《概率论与数理统计》内容指导

一、概率部分

1．概率论的基本概念及预备知识

     随机现象，随机试验E，样本空间，样本点，随机事件A，基本事件{}

     必然事件，不可能事件，随机变量X，随机向量（X,Y ）

     排列：从n个元素中任取m个元素的排列数：

     组合：从n个元素中任取m个元素的组合数：

2．事件间的关系与运算规律

    相互关系：1°  事件B包含A：AÌB（指事件A发生必导致B发生）

                  A与B相等：A＝B（指AÌB且BÌA）

              2°  A与B的和事件：A∪B（指A, B中至少有一个发生）

                  A与B的直和：A＋B＝A∪B（A与B互不相容时）

              3°  A与B的积事件：A∩B 或AB（指A与B同时发生），

              4°  A与B的差事件：A－B＝（指A发生而B不发生）

              5°  A与B互不相容或互斥：A∩B＝Æ．

              6°  A的对立事件：＝U－A．

    运算规律：(1) 交换律：A∪B＝B∪A,  A∩B＝B∩A

              (2) 结合律：A∪(B∪C)＝(A∪B)∪C ，A∩(B∩C)＝(A∩B)∩C

              (3) 分配律：A(B∪C)＝AB∪AC

3．频率的定义与性质

    事件A发生的频率：（nA为n次试验中A发生的次数）

    频率的基本性质：1°（非负性） 对于任一随机事件A，有fn(A)≥0

                    2°（规范性） 对于必然事件，有fn()＝1

                    3°（有限可加性）若A1, A2,…, Ak两两互斥，则

4．概率的定义与性质

    概率的公理化定义：称实值函数P(A)为事件A的概率，如果P(A)满足下述公理：

        公理1（非负性） 对于任一随机事件A，有P(A)≥0

        公理2（规范性） 对于必然事件，有P()＝1

        公理3（完全可加性） 对两两互不相容的事件A1, A2, …,有

    概率的基本性质：1°  P(Æ)＝0； 0≤P(A)≤1；

                    2°（有限可加性）若A1,A2,…, Ak两两互斥，则

                    3° 若AÌB, 则P(B－A)＝P(B)－P(A)，P(B)≥P(A)

5．概率计算公式

    三种典型概率：古典概率计算公式

                  几何概率计算公式

                  条件概率计算公式

    加法定理：P(A∪B)＝P(A)＋P(B)－P(AB)

    概率乘法定理：P(AB)＝P(A)P(B | A)

    全概率公式：

    贝叶斯公式：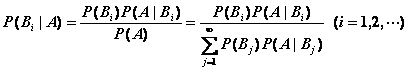

6．等价定理

    等价定理1  对事件A与B，下面四个命题等价

        (1)  A与B相互独立；       (2)  A与相互独立；

        (3)  B与相互独立；              (4)  与相互独立．

    等价定理2  在时，下面四个命题等价

        (1)  A与B相互独立                (2) 

        (3)                  (4)

7．随机变量的概率分布（分布函数、分布律、分布密度）

    分布函数：

    分布律： 

    分布密度：（在f(x)的连续点）

常用分布：

    1）．0-1分布（1次试验中A发生的次数为k，）

    2）．二项分布（n重伯努利试验中A发生的次数为k，）

    3）．泊松分布（时二项分布的逼近分布，）

    4）．均匀分布

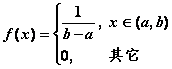
    5）．指数分布

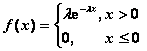
    6）．正态分布

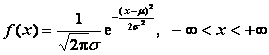
（常用分布的分布律、分布密度、数学期望及方差见《概率统计》附表1）

8．随机向量的概率分布（分布函数、分布律、分布密度）

分布函数：联合分布函数：

              边缘分布函数：FX ( x )＝P { X ≤x }＝F ( x, +¥ )

                            FY ( y )＝P { Y ≤y }＝F ( +¥ , y )

    分布律：  联合分布律：P {X＝x i ,Y＝yj}＝p i j,  i, j＝1, 2, …

                                   

              边缘分布律：

                          

              条件分布律：

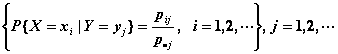
    分布密度：联合分布密度：（在f的连续点）

              边缘分布密度：

              条件分布密度：（在fX (x)大于0的连续点）

                            （在fY ( y )大于0的连续点）

9．构成分布函数、分布律、分布密度的充要条件

    F(x)为分布函数     F(x)单调不减右连续且F(-¥)＝0，F(+¥)＝1

    F(x, y)为分布函数   F(x, y) 关于x和y均单调不减右连续且

                           F(-∞, y)＝F(x,-∞)＝F(-∞,-∞)＝0 , F(+∞,+∞)＝1

    pk为分布律         

    p ij为分布律         

    f (x)为分布密度      

    f (x, y)为分布密度    

10．连续型随机变量的性质

    1°  连续型随机变量的分布函数必连续，但分布函数连续的随机变量未必是连续型的．

    2°  一维（二维）连续型随机变量在任意一点（任意曲线上）取值的概率必为零．

3°  P{a＜X＜b}＝P{a≤X＜b}＝P{a＜X≤b}＝P{a≤X≤b}

＝F(b)－F(a)＝

    4° 对平面区域G, 有

11．随机变量相互独立的等价定理

    随机变量相互独立的等价定理  对于随机向量(X , Y ), 下面五个命题等价

        (1)  X 与 Y 相互独立；

        (2) 所有可能的条件分布律与相应的边缘分布律一致

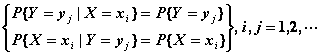
           或 所有可能的条件分布密度与相应的边缘分布密度几乎处处相等．

（几乎处处相等）

（几乎处处相等）

        (3)  或

        (4) 对于任意二实数集S, T，有P{XÎS,YÎT} = P{XÎS} P{YÎT}

        (5) 对于任意二实数x, y, 有F(x, y) = FX(x) FY( y)

12．随机变量函数的重要结论

    1）Y＝g(X )的分布函数  FY(y)＝P{Y≤y}＝P{g(X)≤y}

    2）Z＝g(X,Y)的分布函数 FZ (z)＝P{Z≤z}＝P{g(X ,Y)≤z}

    3）Z＝X＋Y 的分布密度

                                （当X 与Y 相互独立时）

    4）当 X1, X2,…,X n相互独立时，max(X1, X2,…,Xn) 和min(X1, X2,…,Xn) 的分布函数

                           

                          

13．有关正态分布的重要结论

若（正态分布），则 （标准正态分布）

N(m,s 2)与N(0,1)的分布密度分别为：，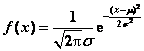

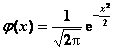
N(m,s 2) 的分布函数与N(0,1)的分布函数满足

，F(-x)＝1－F(x)

    以m1, m2, s1, s2, r 为参数的二维正态随机变量X ,Y的密度函数为

 

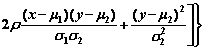
其中的随机变量X 与Y 相互独立的充要条件是 r＝0．

14．随机变量的数字特征

    数学期望的性质与计算：

        1°  

        2°

        3°

        4° 若X1, X2,…,Xn是随机变量，ak是常数，则

        5° 若X1, X2,…,Xn是相互独立的随机变量，则

    方差的性质与计算：

1° DX＝Cov(X ,X)＝E(X－EX )2＝EX 2－(EX)2,  D(C)＝0,  D(CX )＝C2DX

        2° D(X＋Y)＝DX＋DY＋2 Cov(X ,Y)

                  ＝DX＋DY（X, Y 是相互独立）

        3° DX＝0的充要条件是 X以概率1取常数C＝EX．

    协方差的性质与计算：

1° Cov(X ,Y)＝Cov(Y, X )＝E[(X－EX)(Y－EY)]＝E(XY)－(EX )(EY )

2° Cov(a ,X)＝0，Cov(aX ,bY)＝abCov(X , Y)

        3° Cov(X＋Y, Z )＝Cov(X ,Z )＋Cov(Y,Z )．

    相关系数与矩：

        相关系数（当 rXY＝0时称X 与Y 不相关），

        k阶原点矩：EX k ，        k＋l阶混合原点矩：E(X kY l)，

        k阶中心矩：E(X－EX )k ，   k＋l阶混合中心矩：E[(X－EX )k(Y－EY )l]

15．大数定律与中心极限定理

    切比雪夫不等式  设X 具有数学期望EX 与方差DX，则对于任意的正数e , 有

P{|X－EX|≥e }≤   或   P{|X－EX|＜e }≥1－

    辛钦大数定律  设X1,X2,… 相互独立同分布，则, 有

   或   

    伯努利大数定律  设nA是n重伯努利试验中A发生的次数, p=P(A), 则, 有

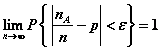   或   

林德伯格-列维（Linderberg-levi）中心极限定理  设 X1,X2,…独立同分布且EXk =m,  ，则

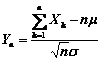
的极限分布是标准正态分布N(0,1)，即对于任意的x，有

  或 

即  

棣莫佛 -拉普拉斯（De Moivre-Laplace）中心极限定理  设X ～B(n, p)

则对于任意的x，有或

即  

 

二、统计部分

1．数理统计的基本概念

总体（母体）：所研究对象（取实数值）的全体．

个体：       组成总体的元素．

样本（子样）：（为样本容量）

样本均值：     

样本方差：     

样本k阶原点矩： 1,2,…

样本k阶中心矩： 1,2,…

频率直方图：   

2．基本分布

1）标准正态分布  若, 则

,

上侧分位数  ：

2）分布  设相互独立且,则

上侧分位数  ：

3）t分布    设与相互独立，且, ，则

～

上侧分位数  ：

4）F分布   设与独立，且,,则

～()

上侧分位数  ：=

3．正态总体的抽样分布

一个正态总体的抽样分布

设总体，为样本容量、样本均值、样本方差，那么

（1）且

（2）与相互独立，且

（3）

两个正态总体的抽样分布

设, ，且它们相互独立，并设分别为他们的样本容量、样本均值、样本方差，那么

（1）

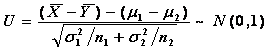
（2）当时，

其中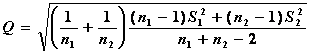

（3）

4．参数的点估计

抽取子样：（样本值为）

1）矩估计法（无需知道总体分布）

矩估计方程：   

解之得矩估计量：

2）最大似然法

(1) 对总体(未知)．构造似然函数：

（离散型总体的分布律）

（连续型总体的分布密度）

令        （对数似然方程）

即可解出（使似然函数取最大值的）最大似然估计值，从而得最大似然估计值量

3）估计量的评价标准

（1）无偏性  设=()是的估计，若, 则称是的无偏估计．

（2）有效性  设估计量与是参数的两个无偏估计量，若，则称较有效．

（3）一致性  设()为参数的一个估计量，若

则称()是的一致估计（相合估计）．

5．参数的区间估计

(1) 选择包含待估参数的正态总体抽样．

(2) 根据正态总体抽样构造大概率事件

(3) 根据大概率事件构造估计区间，正态总体均值与方差（或均值差与方差比）的区间估计表见附表7

6．参数的假设检验

1）假设检验的一般原理

(1) 选择包含检验参数的正态总体抽样．

(2) 根据正态总体抽样构造小概率事件

(3) 根据小概率事件确定拒绝域．

2）假设检验可能犯的两类错误

（1）第一类错误（弃真错误）：原假设正确，但我们却错误地拒绝了它。犯这类错误的概率不超过显著性水平．

（2）第二类错误（纳伪错误）：原假设不正确，但我们却错误地接受了它，犯这类错误的概率记为．