第二节 数列的极限
教学目的:理解数列极限的概念,为研究微积分作好工具准备
教学重点:收敛数列的性质及运算法则
教学难点:数列极限概念的理解及计算
一、数列极限的概念及定义
本节讨论定义域为自然数集N,值域含于实数集R的函数。其函数只可按照变量的顺序排列为
![]() ,
,![]() ,…,
,…,![]() ,…
,…
因此,有下列定义:
定义 设f是定义于N上的一个函数,其函数值按![]() …的顺序排列成一个序列:
…的顺序排列成一个序列:
![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…
,…
就成为数列,简单地记作![]() 。
。![]() 称为数列的第n项或通项,n为脚标.
称为数列的第n项或通项,n为脚标.
例如:

观察上面的几个数列,我们可以发现随着![]() 的无限增大,有的数列无限的趋近一个常数
的无限增大,有的数列无限的趋近一个常数![]() ,有的数列无限增大,而有的数列则与前两种情况不同.数列的极限就是研究在自变量
,有的数列无限增大,而有的数列则与前两种情况不同.数列的极限就是研究在自变量![]() 无限增大这种趋势下,因变量
无限增大这种趋势下,因变量![]() 的变化趋势.当
的变化趋势.当![]() (即
(即![]() 无限增大)时,如果的
无限增大)时,如果的![]() 的变化趋势由一个确切的“目标”
的变化趋势由一个确切的“目标”![]() ,那么常数
,那么常数![]() 就叫做该数列
就叫做该数列![]() 在
在![]() 时的极限.例如:当
时的极限.例如:当![]() 时,
时,![]() 的极限为0,
的极限为0, 的极限也是0,
的极限也是0,![]() 的极限为2,而
的极限为2,而![]() 与
与![]() 没有极限.
没有极限.
如果数列![]() ,当
,当![]() 无限增大时,数列
无限增大时,数列![]() 的取值能无限接近常数
的取值能无限接近常数![]() ,我们就称
,我们就称![]() 是
是![]() 当
当![]() 时的极限,记作
时的极限,记作
![]() .
.
当然,以上的说法 仅仅是数列极限的一种定性描述.我们在研究数列极限时,只凭定性描述和观察很难做到准确无误,特别在理论推导中,以直觉作为推理的依据是不可靠的,因此有必要寻求用精确的、定量化的数学语言来刻画数列的极限.我们注意到在数列极限中“![]() ”,以及“
”,以及“![]() 无限的趋近于
无限的趋近于![]() ”,它主要强调的是“一个过程”以及一种“接近”程度,经过前人的不断总结给出了一下定义.
”,它主要强调的是“一个过程”以及一种“接近”程度,经过前人的不断总结给出了一下定义.
设![]() 为一个数列对于任意给定的正数
为一个数列对于任意给定的正数![]() (不论它多么小),总存在正整数
(不论它多么小),总存在正整数![]() ,使得对于
,使得对于![]() 时的一切
时的一切![]() ,不等式
,不等式
![]()
都成立,则称常数![]() 是数列
是数列![]() 的极限,或者称数列
的极限,或者称数列![]() 收敛于
收敛于![]() ,记为
,记为
![]()
或
![]() .
.
如果数列没有极限,就说数列是发散的.
为了以后论述的方便, 数列极限的定义,常用逻辑符号来表达:
![]() ,使得
,使得![]() ,有
,有![]() .
.
定义中极限![]() (
(![]() 是一个常数)及任意给定的正数
是一个常数)及任意给定的正数![]() ,它确定了
,它确定了![]() 一个领域
一个领域![]() ;总存在正整数
;总存在正整数![]() ,也确定数列
,也确定数列![]() 中的某一项
中的某一项![]() ;只要
;只要![]() ,就有
,就有![]() 成立.即说明从
成立.即说明从![]() 以后的所有项
以后的所有项![]() ,全落入
,全落入![]() 中.
中.
需要指出的是,任意给定的数![]() ,一方面由于
,一方面由于![]() 的任意性,决定了它的取值有无限种的可能,从而可以任意的小,以刻画
的任意性,决定了它的取值有无限种的可能,从而可以任意的小,以刻画![]() 与
与![]() 的无限逼近. 另一方面是
的无限逼近. 另一方面是![]() 的确定性,它是任意给定的,一旦给出后,它就定了,这样就可以找出
的确定性,它是任意给定的,一旦给出后,它就定了,这样就可以找出![]() (即确定出
(即确定出![]() 这一项),使得
这一项),使得![]() 以后的所有项在
以后的所有项在![]() 中,但是
中,但是![]() 不是唯一的,只要保证
不是唯一的,只要保证![]() 存在即可.例如对于某一个
存在即可.例如对于某一个
![]() ,存在正整数
,存在正整数![]() ,只要
,只要![]() ,就有
,就有![]() 成立,那么此时也有:对于上面的
成立,那么此时也有:对于上面的![]() ,
,![]() 是大于
是大于![]() 的确定的正整数(例如
的确定的正整数(例如![]() ),当
),当![]() 时,
时,![]() 也成立.
也成立.
为了更直观的说明![]() 与
与![]() 之间的关系,看下面例题。
之间的关系,看下面例题。
例2-1 用数列极限定义证明![]() 。
。
证 因为 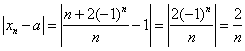 ,
,
![]() ,欲使
,欲使![]() 。只要
。只要![]() ,即
,即![]() ,取
,取![]() (即确定了
(即确定了![]() 这一项),则当
这一项),则当![]() 时,有
时,有
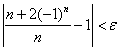
所以
![]()
在以上证明中,当![]() 时,
时,![]() .也就是说从第200项以后,数列的所有项:
.也就是说从第200项以后,数列的所有项:![]() 均满足
均满足![]() 当
当![]() 时,
时,![]() ,
,![]() 的
的![]() 均满足
均满足![]() .需要指出,一般
.需要指出,一般![]() 越小,则
越小,则![]() 越大,但
越大,但![]() 不是唯一的.例如
不是唯一的.例如![]() 时,取
时,取![]() 也行(但
也行(但![]() 则不行,为什么?)。
则不行,为什么?)。
例1-4 设![]() ,证明数列
,证明数列
![]()
的极限是0。
证 因![]()
令![]() ,(由于
,(由于![]() ,故
,故![]() ),
),
则
![]()
所以
![]() .
.
![]() 要使
要使![]() ,只要
,只要![]() ,即
,即![]() ,取
,取![]() ,则当
,则当![]() 时,
时,
有
![]() ,
,
所以
![]()
在以上证明中为了取得N的较简单的表达式,应用了二项式定理。如果从![]() 通过取对数得
通过取对数得![]() ,取
,取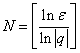 也可以。在用
也可以。在用![]() 定义证明极限时,为了得到N的较为简单的表达式,要对
定义证明极限时,为了得到N的较为简单的表达式,要对![]() 进行适当的放大,其主要手法是使
进行适当的放大,其主要手法是使![]() ,当
,当![]() 时,比较容易地解出
时,比较容易地解出![]() 。
。
例 2-2 用极限定义证明![]()
证 因为
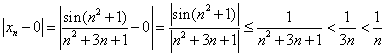
![]() 要使
要使![]() ,只要
,只要![]() ,即
,即![]() 。取
。取![]() ,则对
,则对![]()
有
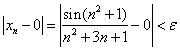
所以
![]()
在以上证明中。我们也可以使![]() 。但若使
。但若使![]() ,那N的表达式就过于繁琐。由于极限定义中的N不唯一,证明时我们力求使N更简单一些。需要指出:一般情况下,用定义只能验证某数是否为某数列的极限,不能用它来求数列的极限,但通过数列的
,那N的表达式就过于繁琐。由于极限定义中的N不唯一,证明时我们力求使N更简单一些。需要指出:一般情况下,用定义只能验证某数是否为某数列的极限,不能用它来求数列的极限,但通过数列的![]() 定义可以证明有关的运算法则及定理,再通过它们来求极限。下面我们介绍极限的运算法则和求极限的一些方法。
定义可以证明有关的运算法则及定理,再通过它们来求极限。下面我们介绍极限的运算法则和求极限的一些方法。
二、收敛数列的性质及运算法则
对于一个数列,如何判断它是否收敛(即极限是否存在)?如果收敛,又怎样求出它的极限?这是极限理论中至关重要的两个基本问题,为此我们必须讨论数列极限的性质及运算法则。
定理 设![]() ,则
,则
(1)![]()
(2)![]()
(3)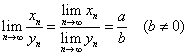
(4)![]() (由此可得)
(由此可得)![]()
(5)![]()
证
(1)仅就![]() 证之。
证之。
由![]() 知:
知:
![]()
![]()
因为
![]()
所以
![]() ,有
,有
![]()
注 证明中出现了![]() 主要是为了体现对同一标准
主要是为了体现对同一标准![]() “速度”的不同。例如
“速度”的不同。例如![]() 。当
。当![]() 时,
时,![]() ,取
,取
![]() ,取
,取![]() 。至于
。至于![]() ,中用
,中用![]() 是为了最后结论与定义一致。
是为了最后结论与定义一致。
(2)、(3)在后面加以证明,(4)、(5)可直接用极限定义证明(读者自证)。
定理 若数列![]() 有界,且
有界,且![]() ,则
,则
![]()
证 由![]() 有界知
有界知![]() ,有
,有![]() ,
,
又由![]() ,可知,
,可知,![]() ,有
,有![]()
因为![]() (当
(当![]() 时)
时)
所以,![]() ,有
,有![]() ,
,
也即![]() .
.
读者也许注意到了,对于一个具体数列我们用定义证明其极限是某个数时,项数N是一个具体的表达式(表达式不惟一)。而对于抽象的数列极限(如以上的法则等)证明,项数N是通过已知数列极限中所得的项数确定的,它们虽然不尽相同,但是目的是为了保证项数N的存在性。用![]() 定义证明一些命题,初学者有一定的难度,下面再介绍夹逼定理。通过该定理可以证明一些数列的收敛性,相对而言,比用
定义证明一些命题,初学者有一定的难度,下面再介绍夹逼定理。通过该定理可以证明一些数列的收敛性,相对而言,比用![]() 定义要简单一些。
定义要简单一些。
定理 (夹逼定理) 已知三数列![]() 满足
满足![]() 且
且![]() 则
则![]()
证 由![]() ,
,![]() 得
得
![]()
![]()
当![]() 时,
时,
![]()
即
![]()
所以![]() 有
有
所以![]() .
.
例
2-3 证明![]() ,
,
证 欲证![]() ,即证
,即证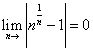
因为![]() 时,
时,![]() ,所以
,所以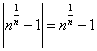
令![]()
即![]()
所以
![]()
即![]()
又因为
![]()
所以![]()
由于![]() ,(读者自己证明)
,(读者自己证明)
所以![]() ,即
,即![]() .
.
定理 (极限的惟一性) 设![]() ,则
,则![]()
证 ![]()
由已知条件可知:
![]() ,所以
,所以![]()
又![]()
由夹逼定理可知
![]()
所以
![]()
定理 (极限的保号性) 设![]() ,且
,且![]() ,则
,则![]() ,有
,有![]() 。
。
证 因![]() ,故
,故![]() 。取
。取![]() ,有
,有![]() ,
,
即![]()
有因为![]() ,所以
,所以![]() ,取
,取![]() ,有
,有![]() ,
,
即![]()
取![]() ,则当
,则当![]() 时,有
时,有
![]()
推论 若![]() 收敛,则
收敛,则![]() 有界.
有界.
证 因为![]() 收敛,即使
收敛,即使![]()
![]()
那么
![]()
由于![]() ,据定理1-2-5可知,
,据定理1-2-5可知,![]() ,
,![]() ,有
,有
![]()
取
![]()
则![]() ,有
,有![]() ,所以
,所以![]() 有界.
有界.
以上的推论表明,有界是数列收敛的必要条件.但是有界数列也不一定收敛,例如![]() 虽然有界,但它发散.
虽然有界,但它发散.
夏我们利用夹逼定理与极限的保号性定理证明极限的乘法、除法运算法则.已知设![]() ,则
,则
(1)![]()
(2)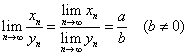
证
(1)因为
![]()
![]()
![]()
又因为
![]()
所以
![]()
又
![]()
所以
![]()
即
![]()
(2)只需证:![]() ,在利用极限的乘法运算法则就可得到除法法则.
,在利用极限的乘法运算法则就可得到除法法则.
因为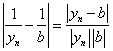
又因为
![]()
所以
![]() ,
,![]()
有
![]()
即![]() ,
,![]() 有
有

因为
![]()
所以
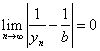
即
![]()
以上“乘法、除法”极限的证明使是夹逼定理的一个应用,其目的是说明有了一些运算法则后,用定义证明一些命题就不是唯一的途径了.
例2-4 证明 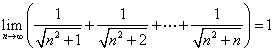
证明:因为
![]()
而
![]()
所以原式极限为1.
例2-5 求![]()
解:
![]()
![]()
![]()
故
![]()