第三节 全微分

教学目的：学习和掌握多元函数（以二元函数为主）全微分的定义，掌握二元函数可微与偏导数存在之间的关系，会求多元函数的全微分。

教学重点：可微与偏导数存在之间的关系，多元函数的全微分。

教学难点：计算多元函数的全微分。

教学内容：

一、全微分的定义

定义 设函数在点的某邻域内有定义，如果函数在点的全增量

                    

可表示为

                     ，

其中、不依赖于、而仅与有关，，则称函数在点可微分，而称为函数在点的全微分，记作，即       .

如果函数在区域内各点处都可微分，那末称这函数在内可微分.

在第二节中曾指出，多元函数在某点的各个偏导数即使都存在，却不能保证函数在该点连续.但是，由上述定义可知，如果函数在点可微分，那末函数在该点必定连续.事实上，这时由（2）式可得

设函数在点的某一邻域内有定义，并设为这邻域内的任意一点，则称这两点的函数值之差为函数在点对应于自变量增量、的全增量，即

                      

2.可微分的条件

定理 （可微的必要条件）若函数在点可微分，则该函数在点的偏导数、必定存在，且函数在点的全微分为

                                       =+.

证 设函数在点可微分.于是，对于点的某个邻域的任意一点，（2）式总成立.特别当 时（2）式也应成立，这时，所以（2）式成为

                .

上式两边各除以，再令而取极限，就得

△x→0
 
             lim=，

从而偏导数存在，且等于. 同样可证=.所以（3）式成立.证毕.

我们知道，一元函数在某点的导数存在是微分存在的充分必要条件.但对于多元函数来说，情形就不同了.当函数的各偏导数都存在时，虽然能形式地写出 +，但它与之差并不一定是较高阶的无穷小，因此它不一定是函数的全微分.换句话说，各偏导数的存在只是全微分存在的必要条件而不是充分条件.例如，函数

           =

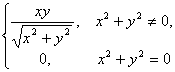
在点处有  及 ，所以

              =,

如果考虑点沿着直线 趋于，则

              ===,

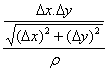它不能随而趋于0，这表示时，

                         

并不是较高阶的无穷小，因此函数在点处的全微分并不存在，即函数在点处是不可微分的.

由定理1及这个例子可知，偏导数存在是可微分的必要条件而不是充分条件.但是，如果再假定函数的各个偏导数连续，则可以证明函数是可微分的，即有下面定理.

定理 （可微的充分条件）  如果函数的偏导数、在点连续，则函数在该点可微分.

证  因为我们只限于讨论在某一区域内有定义的函数（对于偏导数也如此），所以假定偏导数在点连续，就含有偏导数在该点的某一邻域内必然存在的意思（以后凡说到偏导数在某一点连续均应如此理解）.设点为这邻域内任意一点，考察函数的全增量

  

     .

在第一个方括号内的表达式，由于不变，因而可以看作是 的一元函数 的增量.于是，应用拉格郎日中值定理，得到

                   

               =   

又假设，在点  连续，所以上式可写为

               

         =，                                             （4）

其中为、的函数，且当， 时，.

    同理可证第二个方括号内的表达式可写为

             ，                        （5）

其中为 的函数，且当时， .

由（4）、（5）式可见，在偏导数连续的假定下，全增量△z可以表示为

                     .                       （6）

容易看出

                             ||，

它是随着，即而趋于零.

    这就证明了 在点是可微分的.

以上关于二元函数全微分的定义及微分的必要条件和充分条件，可以完全类似的推广到三元和三元以上的多元函数.

习惯上，我们将自变量的增量、分别记作、，并分别称为自变量的微分.这样，函数的全微分就可以写为

                       =+.                                       (7)

例8-15  计算函数的全微分．

解  因为    ＝２，＝，

      所以    ＝２＋．

例8-16  计算函数在点处的全微分．

解  因为  =yexy, =xexy

x=2

y=1
 

x=2

y=1
 
             |   =,  |   =,

        所以 =．

例8-17  计算函数的全微分.

解  因为 =, =+, =,

        所以 =(+ ) +．

小结：本节讨论了多元函数（以二元函数为重点）全微分的定义及存在条件和求法

作业：        

1. 求函数当，时的全微分．

2. 求函数当，，，时的全增量和全微分．

3. 求函数当，，，时的全微分