第三节 格林公式及其应用

教学目的：理解和掌握格林公式及应用

教学重点：格林公式

教学难点：格林公式的应用

教学内容：

一、Green公式

单连通区域.

设为单连通区域，若内任一闭曲线所围的部分都属于.称为单连通区域（不含洞），否则称为复连通区域（含洞）.规定平面的边界曲线的方向，当观看者沿行走时，内在他近处的那一部分总在他的左边，如

定理1. 设闭区域由分段光滑的曲线围成，函数和在上具有一阶连续偏导数，则有=.为的取正向的边界曲线.即格林公式

证：对既为- 型又为-型区域：∵连续，

=

=

： 又

=+

=

∴

对于-型区域，同理可证 = ∴原式成立

对于一般情况，可引进辅助线分成有限个符合上述条件区域，在上应用格林公式相加，由于沿辅助线积分是相互抵消，即可得证.

几何应用，在格林公式中，取，=

∴

说明：1）格林公式对光滑曲线围成的闭区域均成立

2）记法=

3）在一定条件下用二重积分计算曲线积分，在另外条件下用曲线积分计算二重积分.

4）几何应用.

例1． 计算 ：

解： 原式=， ，

例1． 计算星形线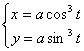围成图形面积

=

二 平面上曲线积分与路径无关的条件

1） 与路无关：是为一开区域，在内具有一阶连续偏导数，若内任意指定两点及内从到的任意两条曲线

恒成立，则称在内与路径无关.否则与路径有关.

例1． ：从到的折线

从到的直线

解：= 3

：,即

=

定理：设，在单连通区域内有连续的一阶偏导数，则以下四个条件相互等价

（1）内任一闭曲线，=.

（2）对内任一曲线，与路径无关

（3）在内存在某一函数使在内成立.

（4），在内处处成立.

证明：（1）（2） 在内任取两点，及连接的任意两条曲线，

∴为内一闭曲线

由（1）知，

即+=

∴=

（2）（3）若在内与路径无关.当起点固定在（）点，终点为后，则是的函数，记为.

下证：=的全微分为=.

∵，连续，只需证， ，

由定义

=+

=+

∴==，

即， 同理.

（3）（4）若=，往证=，，

，， 由具有连续的一阶偏导数

故=

（4）（1）设为内任一闭曲线，为所围成的区域.=

=.

例2．曲线积分， 为过，和点的圆弧.

解： 令，，则，

∴与路径无关.

取积分路径为.

+

==

例2． 计算， （1）为以为心的任何圆周.

（2）为以任何不含原点的闭曲线.

解：（1）令，，

，，

∴在除去处的所有点处有=，做以0为圆心，

为半径作足够小的圆使小圆含在内，∴=，即

=

（2）∵= ∴0

三、二元函数的全微分求积

∵ 与路径无关，则为某一函数的全微分为

==+

注：有无穷多个.

例3． 验证：是某一函数的全微分，并求出一个原函数.

解：令，

，

∴原式在全平面上为某一函数的全微分，取

，

==

例5． 计算， 为从到再到，是半圆弧

解：令，

，，

添加直线，则，原式+=

==

∴原式==

例6．设在上连续可导，求，其中

为从点到的直线段.

解；令，

=

，故原积分与路径无关，添构成闭路，∴原式+

∴原式==

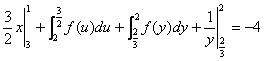
练习：1.证明：若为连续函数，而为无重点的按段光滑的闭曲线，则.

2.确定的值，使在不经过直线的区域上，与路径无关，并求当为从点到点的路径时的值. ，

3．设，为上的连续函数，证明

小结： 1. 格林公式及应用，积分与路径无关的四个等价命题，全微分求积.

2. 格林公式使有些问题简化，有时可计算不封闭曲线积分，只需添上一条线使之成为封闭曲线，再减去所添曲线的积分值即可.

作业：P153 2，3，5