概率统计十问
数学是由两个大类——证明和反例组成,数学发现主要是提出证明和构造反例。从科学性来讲,反例就是推翻错误命题的有效手段;从教学上而言,反例能够加深对正确结论的全面理解。正如美国的B.R.盖尔鲍姆曾说:“一个数学问题用一个反例予以解决给人的刺激犹如一出好的戏剧”,下面我们通过举反例的方式对概率论与数理统计课程中一些疑难问题进行说明,我想看完后大家都会有这一同感!
1、同一问题的概率模型是否唯一?
概率模型（Schema）是随机现象的数学形式，它不是实际问题本身，而是实际问题的数学抽象。对于现实世界中的随机现象，要想进入数学理论的研究，首先必须确定其概率模型。
由于我们的认识水平以及现实问题的复杂性，使得所选定的概率模型往往不是唯一的。
《概率论》中著名的“
个球在个盒子中的分布问题”（见王梓坤《概率论基础及其应用》P12-13科学出版社）就说明了这一情况，这是一个典型概率模型的问题，内容是：设有
个球，每个都能以相同概率
落到个盒子（
）的每一个盒子中，求指定的某个盒子中各有一个球的概率。
如果我们把个球看作个人，而把个盒子视为一年的天数：
。这时上述问题就成为了概率论中一个颇为著名问题的概率模型。此问题就是求参加某次集会的几个人中，没有n个人生日相同的概率。
众所周知，球彼此之间可以认为是有区别，也可以认为无区别；一个盒子可以假定仅能容纳一个球，也可以允许它能容纳许多球，如此一来，就可以分为以下几种概率模型：
（1）马克斯威尔－波尔茨曼认为球彼此之间有区别，且对每盒中可容纳球数不加限制；
（2）玻色－爱因斯坦认为球彼此不能区别，且对每盒中可容纳球数不加限制；
（3）费密－狄雷克认为球彼此无区别，且限制每盒中不能同时容纳二个球。
后来，为了统一以上三种情况，又产生了第四种情况
（4）布里龙认为球彼此可以区别，且增加了一些其他条件限制（见杨宗磐《概率论入门》P.13科学出版社）。
以上四种情况，形成了统计物理学中的四种统计模型：球可看作为质点，盒子看作状态。
再看一例：个人围成一个圆周，求其中甲和乙两人之间恰好有
个人的概率（圆周排列时，仅考虑从甲到乙的顺时针方向）。对此问题，至少可用三种概率模型来处理,即可以构造如下的三种随机试验：
（1）个人的任意一种排列作为一个基本事件；
（2）仅以甲、乙两人在个人一行中的不同排法作为基本事件组；
（3）可由甲和乙之间的间隔数来考虑。
不论取何种概率模型，本题所求概率均为
。
2、概率为零的事件一定是不可能事件吗?
不可能事件的概率必为零，反之却未必成立。例如,当考虑的概率模型为古典概率模型时，概率为零的事件一定是不可能事件;当考虑的概率模型是几何概率模型时，概率为零的事件未必是一个不可能事件。例如：设试验
为“随机地向边长为
的正方形内投点”，事件
为“点投在正方形的一条对角线上”（见下图）
1 
|
|
0
1 
此时
尽管
但却可能发生，另外，对于连续性随机变量，它在某固定点取值的概率为零，但它不是不可能发生。由对立事件知，概率为的事件未必是必然事件。
3、试验次数多概率就一定大吗?
在概率论的萌芽时期，有一个著名的问题：一颗骰子掷4次至少得一个1点，与两颗骰子掷24次至少得两个1点，这两个事件究竟哪个发生的概率大？曾引起很多人的注意。现在看来，利用独立试验概率模型容易求出它们的概率。
次独立重复试验中事件至少发生一次的概率为
，其中
，现考虑欲使
，则
，此式给出了的下界，使问题得以解决。
以掷一颗骰子作试验，要连续掷次使
点至少出现一次的概率大于等于
,则
。以掷两颗骰子作试验，要连续掷次使两个点至少出现一次的概率大于等于,则
。由此得出，一颗骰子掷
次至少有一个点的概率大于等于,而两颗骰子掷
次至少有一次得两个点的概率小于。
本例表明试验次数多概率不一定就大。
4、事件概率与试验的先后次序是否有关?
设有一口袋，内有
个黑球，
个白球，他们除颜色不同外没有其它不同之处，现把球一个个地摸出，求第
次摸出的是黑球的概率 
。
初看题目，很可能会认为所求概率与摸球次序有关，若那样的话，体育比赛中先后抽签者中签的机会就不均等了，这与我们日常生活中的经验不符，通过具体计算亦可看出所求概率与摸球次序无关。
按自然顺序给球编号，不妨先给黑球编号，再给白球编号，取样空间为第次摸出的球的全部可能的结果，则
表示第次摸出第
号球，
，于是要求的是事件
的概率。由古典概率模型知
,
显然与无关。
本题可用多种方法求解，这里介绍的是最简单的一种，本题存在多种解法的原因，在于一个随机现象有时可用不同的样本空间来描述，所以称本解法是最简单的，因为解法中的样本空间是最小的。
5、既非离散型又非连续型的分布函数是否存在
有，请看下例：设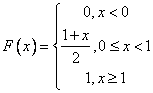
,则由分布函数的定义可知
是分布函数，与对应的随机变量不是取有限个或可列多个值，故不是离散型的分布函数，又因
故也不是连续的分布函数。
6、与不独立，那么与是否有相同分布?
观察
的联合分布及其边缘分布:
|
|
0 |
1 |
2 |
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
由于
,
所以与不独立，但与有相同分布。
7、如果事件与独立，那么与是否是互不相容的呢?
独立性是问题间的概率属性，相容性则是事件间本身的关系。由此不难可知，由独立性推不出互不相容性。请看如下一个命题：若与为两个独立事件，且
,
,但与不是互不相容的。用反证法证明此命题。若
,则
,与独立，且,得
,矛盾，因而
。
由此可见,在本命题的条件下，与独立和与互不相容不能同时成立。但若,中有一个概率为
，则与独立和与互不相容可同时成立。
8、随机变量X的函数的期望是否等于X的期望的函数?
一般
。
例如：设服从如下分布：
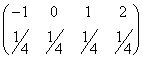
再设
,于是随机变量函数服从如下分布:
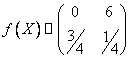
故得
,由于
，可得
,
所以。
9、若有
,则
与独立吗?
若随机变量与独立，且各自数学期望存在，则,反之不真。
例如：设随机变量
服从
上的均匀分布,且
于是
于是，由于与满足
,所以与不独立。
10、零假设与备择假设的地位对等吗?
在假设检验中，首先要根据具体问题提出零假设
和备择假设
，由于零假设是作为检验的前提而提出来的，因此，零假设通常应受到保护，没有充足的证据是不能被拒绝的，而备择假设只有当零假设被拒绝后，才能被接受，这就决定了零假设与备择假设不是处于对等的地位。
下面举例说明交换零假设与备择假设可能会得出截然相反的检验结论。
问题:某厂方断言，本厂生产的小型电动机在正常负载条件下平均电流不会超过0.8A,随机抽取该型号电动机16台，发现其平均电流为0.92A，而由该样本求出的标准差是0.32A，假定这种电动机的工作电流服从正态分布，问根据这一抽样结果，能否否定厂方断言？（取显著性水平
）
解：本题假定
未知，以厂方断言作为零假设，则得假设检验问题：:
;:
。
此时
,
,
,，由t检验法可知拒绝域为
，由于
，故不应该拒绝零假设，即在所给数据和检验水平下，没有充分理由否定厂方的断言。
现在若把厂方断言的对立面（即）作为零假设，则得假设检验问题：
:;:
由t检验法，此时的拒绝域为
因为观测值
，所以应接受零假设，即接受厂方断言的对立面。
由此可见，随着问题提法的不同，得出了截然相反的结论，这一点会使初学者感到迷惑不解，实际上，这里有个着眼点不同的问题，当把“厂方断言正确”作为零假设时，我们根据该厂以往的表现和信誉，对其断言已有了较大的信任，只有很不利于它的观察结果才能改变我们的看法，因而一般难以拒绝这个断言，反之，当把“厂方断言不正确”作为零假设时，我们一开始就对该厂产品抱怀疑态度，只有很有利于该厂的观察结果，才能改变我们的看法，因此，在所得观察数据并非决定性地偏于一方时，我们的着眼点(即最初立场)决定了所得的结论。
打一个通俗的比喻：某人是嫌疑犯，有些不利于他的证据，但并非是起决定性作用的，若我们要求“只有决定性的不利于他的证据才能判他有罪“，则他将被判为无罪，反之，若要”只有决定性的有利于他的证据才能判他无罪“，则他将被判有罪，在这里，也是着眼
点的不同决定了看法，这类事件在日常生活中并不少见，原本不足为奇了。