第1章 绪 论
习 题
1-1 从力学分析意义上说流体和固体有何不同?
1-2 量纲与单位是同一概念吗?
1-3 流体的容重和密度有何区别与联系?
1-4水的密度为
1-5 体积为
 1-6 水的容重g = 9.71 kN/m3,m = 0.599 ´ 10-3 Pa×s,求它的运动粘滞系数。
1-6 水的容重g = 9.71 kN/m3,m = 0.599 ´ 10-3 Pa×s,求它的运动粘滞系数。
 1-7 如图所示为一0.8 ´
1-7 如图所示为一0.8 ´
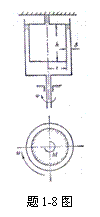
1-8 旋转圆筒粘度计,悬挂着的内圆筒半径r =
1-9 一圆锥体绕其中心轴作等角速度w = 16 rad/s旋转,锥体与固定壁面的间隙d =
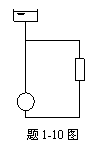
1-10 如图所示为一水暖系统,为了防止水温升高时体积膨胀将水管胀裂,在系统顶部设一膨胀水箱。若系统内水的总体积为
1-11 水在常温下,由5at压强增加到10at压强时,密度改变多少?
1-12 容积为4的水,当压强增加了5at时容积减少

![]()
![]()
第2章 流体运动学基础
习 题
2-1 给定速度场ux = x + y,uy = x - y,uz = 0,且令t = 0时x = a,y = b,z = c,求质点空间分布。
2-2 已知拉格朗日速度分布ux = -b (a sinb t + b cosb t) ,uy =b (a cosb t - bsinb t) ,uz =a 。如t = 0时x = a,y = b,z = c,试用欧拉变量表示上述流场速度分布,并求流场加速度分布,式中a,b,a,b,c为常数。
2-3 已知平面速度场ux = x + t,uy = - y + t,并令t = 0时x = a,y = b,求(1)流线方程及t = 0时过(-1,-1)点的流线;(2)迹线方程及t = 0时过(-1,-1)点的迹线。
2-4设![]() ,说明以下三种导数
,说明以下三种导数
![]()
的物理意义。
2-5 给定速度场ux = -k y,uy = k x,uz = 0,求通过x = a,y = b,z = c点的流线,式中k为常数。
2-6已知有旋流动的速度场为ux = 2y +3z,uy = 2 z +3x,uz = 2x +3y。试求旋转角速度,角变形速度和涡线方程。
2-7 求出下述流场的角变形速度,涡量和线变形速度。并说明运动是否有旋?
ux =U(h2 - y2),uy = uz = 0 。
第3章 流体静力学
习 题

3-1 某水塔,若z =
γ1
3-2
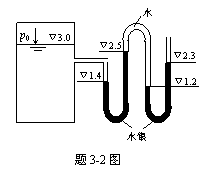
图示复式水银测压计,液面高程如图中所示,单位为m。试计算水箱表面的绝对压强值p0。
h4
3-3
密封容器内注有三种互不相混的液体,求压力表读数为多少时,测压管中液面可上升到容器顶部。

 3-4 图示贮液容器左侧是比重为0.8的油,其上真空计读数为pv=3.0N/cm2;右侧为水,其上压力表读数p=2N/cm2。压差计中工作液体的比重为1.6,求A点的高程。图中高程以m计。
3-4 图示贮液容器左侧是比重为0.8的油,其上真空计读数为pv=3.0N/cm2;右侧为水,其上压力表读数p=2N/cm2。压差计中工作液体的比重为1.6,求A点的高程。图中高程以m计。
 3-5 盛同种液体的两容器,用两根U形管连接。上部压差计A内盛重度为
3-5 盛同种液体的两容器,用两根U形管连接。上部压差计A内盛重度为![]()
的液体,读数为hA;下部压差计B内盛重度为![]() 的液体,读数为hB。求容器内液体的重度
的液体,读数为hB。求容器内液体的重度![]() 。
。
3-6 一容器内盛有重度![]() 的液体,该容器长度L为
的液体,该容器长度L为
3-7 一圆柱形容器静止时盛水深度H=
3-8 圆柱筒盛有重度g = 11.7 KN/m3的液体,今绕铅垂中心轴作等角速度旋转,转速n=200 rpm。已知液体内A点压强pA = 19.61 KN/cm2,至旋转轴的水平距离gA =
γ1 γ2
3-9
直径D=
(1)容器以等加速度a =
(2)容器以转速n = 30 rpm绕铅直中心轴旋转运动,容器底的压强分布规律,并求出其最大和最小压强值。
3-10 某物体在空气中重G = 400N,而在水中重![]() N。求该物体的体积和它的比重。
N。求该物体的体积和它的比重。
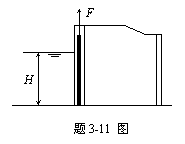
3-11 图示平板闸门,已知水深H =
3-12 图示矩形闸门,高a =
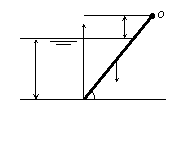

3-13 某倾斜装置的矩形闸门,宽b = ![]() = 60°,铰链o点位于水面以上a =
= 60°,铰链o点位于水面以上a =
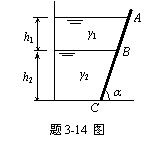
3-14 容器内注有互不相混的两种液体:h1=
 3-15 已知弧形闸门上游水深H1 =
3-15 已知弧形闸门上游水深H1 =
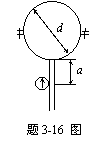
3-16 由两个空心半球组成的密封水箱,球直径d =
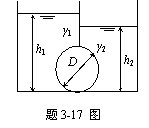 3-17 容器内有一隔板,隔板下部为宽b =
3-17 容器内有一隔板,隔板下部为宽b =![]() ,h1=
,h1=![]() ,h2=
,h2=
第4章 流体动力学基本方程
习 题
4-1 试证下述不可压流体的运动是可能存在的:
(1) ux = 2x2 + y,uy = 2y2 + z,uz = -4 (x + y) z + xy;
(2) ![]()
(3) ux = yzt, uy = xzt, uz = xyt。
4-2 试证不可压流体的运动 ux = x, uy = y, uz = z 不可能存在。
4-3 求使下列速度场成为不可压缩流体流动的条件:
(1) ux = a1x + b1y + c1z, uy = a2x + b2y + c2z , uz = a3x + b3y + c3z;
(2) ux = a xy, uy = b yz, uz = c yz + dz2 。
4-4 设某一流体流场:ux = 2y + 3z, uy = 3z + x , uz = 2x + 4y ,该流场的粘性系数
m = 0.008 Pa×s,求其切应力。
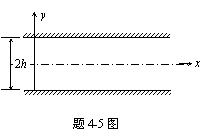 4-5 设两无限大平板之间的距离为2h,其间充满不可压缩流体,如图所示,试给出其运动所满足的微分方程。
4-5 设两无限大平板之间的距离为2h,其间充满不可压缩流体,如图所示,试给出其运动所满足的微分方程。
4-6 试述满足伯努利方程![]() 的条件。
的条件。
第5章 相似原理与量纲分析
习 题
5-1 试将下列各组物理量组合成无量纲量:
(1)t0 、u 、r ; (2)Dp 、u 、g 、 g ;
(3)F 、r 、l 、u ; (4)u 、l 、r 、s ;
(5)u 、l 、t ; (6)r 、u 、m 、l ;
(7)g 、u 、r 、l 。
5-2 如果一个球通过流体时的运动阻力是流体的密度r 、粘度m 、球的半径r及速度u的函数,试用量纲分析法证明阻力R可由下式给出:
![]()
5-3 假设流量Q与管径D、喉道直径d、流体密度r、压强差Dp及流体的动力粘滞系数m有关,试用p 定理分析文丘里管的流量表达式。
5-4 若模型流动与原型流动同时满足Re相似律和Fr相似律,试确定两种流动介质运动粘性系数的关系。
 5-5 一个圆球放在流速为
5-5 一个圆球放在流速为
5-6 当水温为
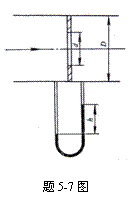
5-7 用水校验测量空气流量的孔板,孔板直径d =
(1) 当孔板用来测定空气流量时,最小流量是多少?
(2)
相应该流量下的水银压差计的读数是多少?设水与空气的温度都是
5-8 为了决定吸风口附近的流速分布,取比例为10作模型设计。模型吸风口的流速为
5-9 溢水堰模型设计比例为20。当在模型上测得模型流量为
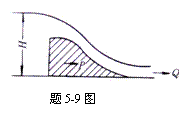
Qm =
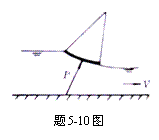
5-10 采用长度比尺为1:25的模型来研究弧形闸下出流,重力为主要作用力。如在模型上量得出口流速为um=
5-11 一建筑物模型在风速为
第6章 理想流体的平面无旋运动
习 题
6-1 给定平面流速度场ux = x2y + y2,uy = x2 - y2x,问:
(1) 是否存在不可压缩流函数和速度势函数;
(2) 如存在,给出它们的具体形式;
(3) 写出微团变形速率各分量和旋转角速度各分量。
6-2 已知不可压缩流体平面流在y方向的速度分量为uy = y2 -2x + 2y,求速度在x方向的分量。
6-3 对平面不可压缩流体的运动,试证明:
(1) 如运动为无旋运动,则必满足Ñ2ux = 0,Ñ2uy = 0;
(2) 满足Ñ2ux = 0,Ñ2uy = 0的流动不一定是无旋流。
6-4 已知平面流动的速度分布为![]() 其中c为常数。求流函数并画出若干条的流线。
其中c为常数。求流函数并画出若干条的流线。
6-5 已知平面流动流函数
![]()
判断是否是无旋流动。
6-6 已知速度势j ,求相应的流函数y :
(1) j = xy ;
(2) j = x3 - 3xy2 ;
(3)
![]() 。
。
6-7 证明j = 1/2(x2 - y2) + 2x - 3y所表示的流场和y = xy + 3x + 2y所表示的流场完全相同。
 6-8 强度为
6-8 强度为
6-9 在速度为u =
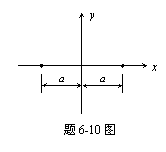
6-10 如图所示,等强度两源流位于x轴,距原点为a。求流函数,并确定滞止点位置。
第7章 粘性管流
第8章 边界层与绕流阻力
习题
8-1 设平板层流边界层中流速分布为线性关系,即![]() ,用动量方程求边界层特性d /d 1,d 1/d 2 。
,用动量方程求边界层特性d /d 1,d 1/d 2 。
8-2 空气以
8-3 光滑平板宽
8-4 求平板绕流层流边界层的总阻力系数CD,及d,d 1,d 2。设边界层中的速度分布为 ![]() 。[提示:先根据速度分布边界条件决定a、b值]
。[提示:先根据速度分布边界条件决定a、b值]
8-5 一平行放置于流速为
(1) 设为层流边界层;
(2) 设为紊流边界层。
8-6 在Re数相等的条件下,
8-7 汽车以
8-8 球形尘粒的密度为
8-9 已知煤粉炉炉膛中上升烟气流的最小速度为
8-10 在气力输送管道中,为了输送一定量的悬浮砂粒,要求风速u0为悬浮速度的5倍,已知砂粒粒径d =
9 明渠流动
习 题
9-1 梯形断面渠道,已知b=
9-2 有一浆砌块石的矩形断面长渠道,已知底宽b=
9-3 坚实粘土的梯形断面渠道,b=
9-4 混凝土排水管,直径d=
①管道满流时的流速和流量;
②充满度![]() 时的流速和流量。
时的流速和流量。
9-5 梯形断面长渠道,流量Q=
9-6 今欲开挖一梯形断面土渠,已知流量Q=
9-7 梯形断面渠道,Q=![]() 设计渠道断面尺寸。
设计渠道断面尺寸。
9-8 情况良好的梯形断面土渠,流量Q=
 9-9 一小河的断面形状及尺寸如图示。流动近似为均匀流,底坡i=0.0004,边滩糙率n1=0.04,主槽糙率n2=0.03,求通过流量(边滩与主槽分别看成矩形断面)。
9-9 一小河的断面形状及尺寸如图示。流动近似为均匀流,底坡i=0.0004,边滩糙率n1=0.04,主槽糙率n2=0.03,求通过流量(边滩与主槽分别看成矩形断面)。
题9-9 图
9-10 渠道某断面的过水面积![]() ,最大水深h=
,最大水深h=
9-11 等腰三角形断面的灌溉渠道,水深为H时,流速![]() 。求临界水深和临界流速。
。求临界水深和临界流速。
9-12 梯形断面长渠道,已知流量Q=![]() 。用几种方法判别流态。
。用几种方法判别流态。
9-13 矩形断面棱柱形渠道,底宽b=![]() ,当流量Q=
,当流量Q=![]() m。试计算跃前水深
m。试计算跃前水深![]() 和水跃能量损失。
和水跃能量损失。
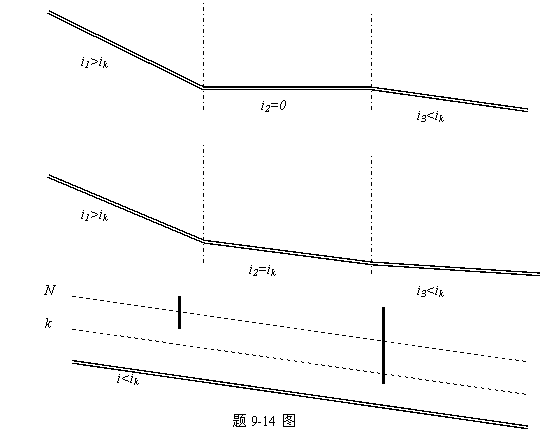
9-14 定性分析棱柱形长渠道中可能产生的水面曲线。
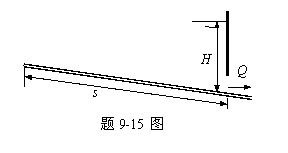 9-15 有一梯形断面渠道,长度s=
9-15 有一梯形断面渠道,长度s=
第10章 孔口管嘴、堰流与闸孔出流
习 题
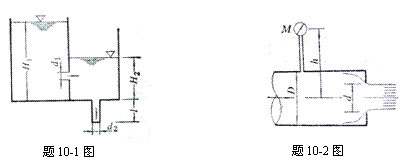
10-1 两水箱用一直径d1=
10-2 管道直径D=
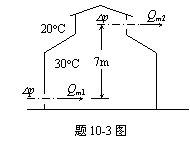
10-3 应用描述气体的能量方程,求解厂房自然通风换气质量流量。已知室内空气温度为
 10-4 矩形断面水槽宽B=
10-4 矩形断面水槽宽B=![]() ,求水头H=
,求水头H=
10-5 已知完全堰的堰宽b=
10-6 直角三角堰自由出流,若堰顶水头增加一倍,流量如何变化?
10-7 直角进口无侧收缩宽顶堰,堰宽b=![]() ,水头H=
,水头H=
10-8 圆角进口无侧收缩宽顶堰,堰高![]() ,堰顶水头H=
,堰顶水头H=
10-9 圆角进口无侧收缩宽顶堰,流量Q=![]() ,下游水深h=
,下游水深h=
10-10 平底平板闸门。已知水头H=
10-11 某水利枢纽设平底冲沙闸,用弧形闸门控制流量,如图10-17。闸孔宽b=
10-12 实用堰顶部设平板闸门以调节上游水位。闸门底缘的斜面朝向上游倾斜角为
60°,如图10-16。试求所需的闸孔开度。已知流量Q=
10-13 一溢流坝为曲线型实用堰,今在坝顶设弧形闸门。已知闸前水头H=
第12章 紊流射流
习 题
12-1 一直径D
=
12-2 某体育馆圆柱形送风口,d0 =
12-3 有一个两面收缩均匀的矩形孔口,截面面积0.05´
12-4 已知空气淋浴喷口直径D =
12-5 车间高
12-6 某锅炉喷燃气的圆形喷嘴,直径为
12-7 温度为
12-8 高出地面
12-9 喷出清洁空气的平面射流,射入含尘浓度为0.12 mg/l的静止空气中。要求距喷口
12-10 试求距R0 =
第13章 一元气体动力学基础
习 题
13-1 空气的压强为101.3kPa,温度为
13-2 空气从储气罐出流,气罐内压力1.5´105Pa,温度为
13-3 某一绝热气流的马赫数M
= 0.8,并已知其滞止压力p0
= 5´98100Pa,温度t0 =
13-4喷管中空气流的速度为
13-5设某储气箱在抽风机作用下保持箱内压强p=99 kPa,外部大气(p0=101.3 kPa,T0=300 K,R=287.06 J/kg× K)通过d=
13-6空气通过等截面短管被吸入容器内,流动条件如图所示,求短管与容器的交接面上的马赫数,密度,质量流量。

13-7 压缩空气从气罐进入管道,已知气罐中的绝对压强p0=7个大气压,t0=
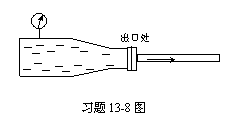
13-8一收缩形喷管用来使容器内空气等熵地膨胀到大气压。容器内的压强和温度分别为147 kPa和
13-9
13-10 空气温度为
13-11 空气在水平管中流动,管长
