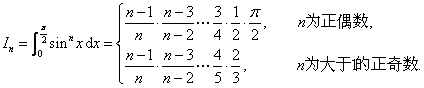第一节
定积分的换元法与分部积分法
教学目的:熟悉定积分的换元法和分部积分法
教学重点:定积分换元法与分部积分法
教学难点:定积分换元法的运用
教学内容:
一、定积分的换元法
定理 假设函数![]() 在
在![]() 上连续,函数
上连续,函数![]() 满足条件:
满足条件:
(1)![]()
![]()
(2)![]() 在
在![]() (或
(或![]() )上具有连续导数,且其值不越出
)上具有连续导数,且其值不越出![]() ,则有
,则有 ![]()
例1 计算下列定积分:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() .
.
解:(1)设![]() ,则
,则![]() ,且当
,且当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故 ![]()
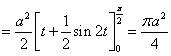
注:换元公式也可以反过来使用,即![]() .
.
(2)设![]() ,则
,则![]()
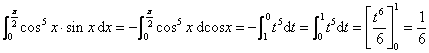
(3)![]()
![]()
![]()
(4)设![]() ,则
,则![]() ,且 当
,且 当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故 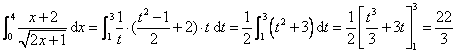
例2 若![]() 在
在![]() 上连续, 证明:
上连续, 证明:
(1)当![]() 为偶函数时,
为偶函数时,![]() ;
;
(2)当![]() 为奇函数时,
为奇函数时,![]() .
.
证:![]()
![]()
(1)当![]() 为偶函数时,
为偶函数时,![]() ,所以
,所以 ![]() ;
;
(2)当![]() 为奇函数时,
为奇函数时,![]() ,所以
,所以 ![]() .
.
例3 若![]() 在
在![]() 上连续,证明:
上连续,证明:
(1)![]() ;(2)
;(2)![]() ,
,
且由此计算![]() .
.
证:(1)设![]() ,则
,则![]() ,且当
,且当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故
![]()
(2)设![]() ,则
,则![]() ,且当
,且当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故 ![]()
所以 ![]()
(3)利用此公式可得:
![]()
例4 设函数![]()
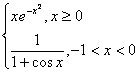 ,计算
,计算 ![]() .
.
解:设![]()
![]()
![]()
二、定积分的分部积分法
定理 设![]() 在
在![]() 上具有连续导数
上具有连续导数![]() ,则
,则
![]()
即
![]() .
.
这就是定积分的分步积分公式.
例1 计算定积分:(1)![]() ;(2)
;(2)![]() .
.
解:(1)设![]() ,
,![]() 则
则
![]()
(2)设![]() ,则
,则
![]()
例2 证明定积分公式:
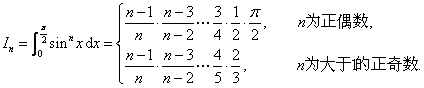
证:设![]() ,则由分步积分公式可得:
,则由分步积分公式可得:
![]()
![]()
故 ![]()
由此递推公式即得: