第一节 定积分在物理学上的应用

一、变力沿直线所作的功

例1 半径为的球沉入水中，球的上部与水面相切，球的比重为 ，现将这球从水中取出，需作多少功?

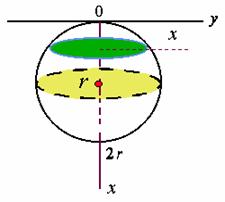
解：建立如图所示的坐标系

将高为的球缺取出水面，所需的力为：

其中：是球的重力，表示将球缺取出之

后，仍浸在水中的另一部分球缺所受的浮力.

由球缺公式 有

从而

十分明显，表示取出水面的球缺的重力. 即：仅有重力作功，而浮力并未作功，且这是一个变力. 从水中将球取出所作的功等于变力从改变至时所作的功.

取为积分变量，则，对于上的任一小区间，变力从到这段距离内所作的功

这就是功元素，并且功为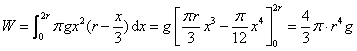

二、水压力

在水深为处的压强为，这里是水的比重.如果有一面积为的平板水平地放置在水深处，那末平板一侧所受的水压力为.若平板非水平地放置在水中，那么由于水深不同之处的压强不相等。此时，平板一侧所受的水压力就必须使用定积分来计算。

例2 边长为和的矩形薄板，与水面成角斜沉于水中，长边平行于水面而位于水深处。设，水的比重为，试求薄板所受的水压力。

解：由于薄板与水面成角斜放置于水中，则它位于水中最深的位置是.

取为积分变量， 则 (注意：表示水深).在中任取一小区间，与此小区间相对应的薄板上一个小窄条形的面积是 ，它所承受的水压力约为 ，于是，压力元素为

这一结果的实际意义十分明显：正好是薄板水平放置在深度为的水中时所受到的压力；而是将薄板斜放置所产生的压力，它相当于将薄板水平放置在深度为处所受的水压力.

三、引力

由物理学知道：质量为、，相距为的两质点间的引力大小为

为引力系数。引力的方向沿着两质点的连线方向。

如果要计算一根细棒对一个质点的引力，由于细棒上各点与该质点的距离是变化的，且各点对该质点的引力方向也是变化的，便不能简单地用上述公式来作计算了。

例3 设有一半径为， 中心角为的圆弧形细棒， 其线密度为常数， 在圆心处有一质量为的质点， 试求这细棒对质点的引力。

解决这类问题，一般来说，应选择一个适当的坐标系。