第一节 向量及其线性运算

教学目的：将学生的思维由平面引导到空间，使学生明确学习空间解析几何的意义和目的.

教学重点：1.空间直角坐标系的概念

2.空间两点间的距离

教学难点：空间思想的建立

教学内容：

一．向量的概念

● 向量：既有大小，又有方向的量；

● 在数学上用有向线段来表示向量，其长度表示向量的大小，其方向表示向量的方向；

● 在数学上只研究与起点无关的自由向量（以后简称向量）；

● 向量的表示方法有a、i、F、等等.

● 向量相等a=b：如果两个向量大小相等，方向相同（即经过平移后能完全重合的向量）.

● 向量的模：向量的大小，记为、.

● 模为1的向量叫单位向量、模为零的向量叫零向量.零向量的方向是任意的.

● 向量平行a∥b：两个非零向量如果它们的方向相同或相反.零向量与如何向量都平行.

二．向量的线性运算

● 加减法：三角形法则及平行四边形法则、其满足的运算规律有交换率和结合率

● 向量与数的乘法：.其满足的运算规律有结合率、分配率.设表示与非零向量a同方向的单位向量，那么

● 定理1：设向量a≠0，那么，向量b平行于a的充分必要条件是：存在唯一的实数λ，使b＝

● 例子：

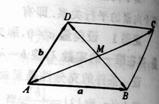
例1：在平行四边形ABCD中，设，，试用a和b表示向量、、和，这里M是平行四边形对角线的交点.（图7－4）

图 7－4

小结：本节讲述了空间解析几何的重要性以及向量代数的初步知识，引导学生对向量（自由向量）有清楚的理解，并会进行相应的加减、乘数、求单位向量等向量运算.

三．空间直角坐标系

1. 将数轴（一维）、平面直角坐标系（二维）进一步推广建立空间直角坐标系（三维）如图7－1，其符合右手规则.

2. 各轴名称，坐标面的概念以及卦限的划分如图7－2所示.

3. 空间点M(x,y,z)的坐标表示方法，关于坐标轴、坐标面原点的对称点的表示法.通过坐标把空间的点与一个有序数组对应起来.

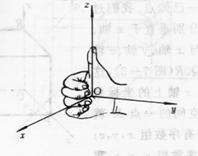
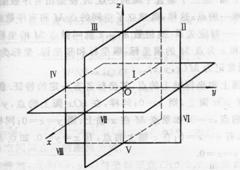
图 7－1 图 7－2

空间两点间的距离

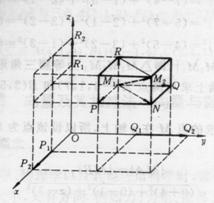
若M₁(x₁,y₁,z₁)、M₂(x₂,y₂,z₂)为空间两点，

则距离（见图7－3）为

图 7－3

一．向量在轴上的投影

1. 几个概念

● 轴上有向线段的值：设有一轴u，是轴u上的有向线段，如果数满足，且当与轴u同向时是正的，当与轴u反同向时是负的，那么数叫做轴u上有向线段的值，记做AB，即.设e是与u轴同方向的单位向量，则

● 设A、B、C是u轴上任意三点，不论三点的相互位置如何，总有

● 两向量夹角的概念：设有两个非零向量a和b，任取空间一点O，作，，规定不超过的称为向量a和b的夹角，记为.

● 空间一点A在轴u上的投影：通过点A作轴u的垂直平面，该平面与轴u的交点叫做点A在轴u上的投影.

● 向量在轴u上的投影：设已知向量的起点A和终点B在轴u上的投影分别为点和，那么轴u上的有向线段的值叫做向量在轴u上的投影，记做.

2. 投影定理

● 性质1：向量在轴u上的投影等于向量的模乘以轴与向量的夹角的余弦：

● 性质2：两个向量的和在轴上的投影等于两个向量在该轴上的投影的和，即

● 性质3：向量与数的乘法在轴上的投影等于向量在轴上的投影与数的乘法.即

二．向量在坐标系上的分向量与向量的坐标

1． 向量在坐标系上的分向量与向量的坐标

通过坐标法，使平面上或空间的点与有序数组之间建立了一一对应关系，同样地，为了沟通数与向量的研究，需要建立向量与有序数之间的对应关系.

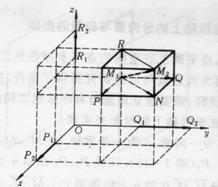
设a =是以为起点、为终点的向量，i、j、k分别表示沿x，y，z轴正向的单位向量，并称它们为这一坐标系的基本单位向量，由图7－5，并应 图 7－5

用向量的加法规则知：

i + j+k

或 a = a_x i + a_yj + a_zk

上式称为向量a按基本单位向量的分解式.

有序数组a_x、a_y、a_z与向量a一一对应，向量a在三条坐标轴上的投影a_x、a_y、a_z就叫做向量a的坐标，并记为

a ＝ {a_x，a_y，a_z}.

上式叫做向量a的坐标表示式.

于是，起点为终点为的向量可以表示为

特别地，点对于原点O的向径

※ 注意：向量在坐标轴上的分向量与向量在坐标轴上的投影有本质区别.

向量a在坐标轴上的投影是三个数a_x、a_y、a_z，

向量a在坐标轴上的分向量是三个向量a_x i 、 a_yj 、 a_zk.

2．向量运算的坐标表示

设a = {a_x，a_y，a_z}，b = {b_x，b_y，b_z}即a = a_x i + a_yj + a_zk，b = b_x i +b_y j +b_zk

则

◆ 加法： a + b = （a_x+ b_x）i +（a_y + b_y） j +（a_z + b_z）k

◆ 减法： a―b = （a_x－b_x ）i + （a_y－b_y） j +（ a_z－b_z ）k

◆ 乘数： λa = (λa_x )i + (λa_y)j + (λa_z)k

◆ 或 a + b ={ a_x+ b_x，a_y + b_y，a_z + b_z }

a－b ={ a_x－b_x，a_y－b_y，a_z－b_z }

λa = {λa_x，λa_y，λa_z}

◆ 平行：若a≠0时，向量b∥a相当于b ＝λa，即

{b_x，b_y，b_z} =λ{a_x，a_y，a_z}

也相当于向量的对应坐标成比例即

四、向量的投影、模、方向角

向量的模与方向余弦的坐标表示式

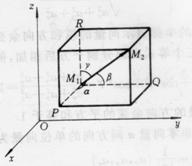设a = {a_x，a_y，a_z}，可以用它与三个坐标轴的夹角（均大于等于0，小于等于）来表示它的方向，称为非零向量a的方向角，见图7－6，其余弦表示形式称为方向余弦.

1． 模

图 7－6

2． 方向余弦

由性质1知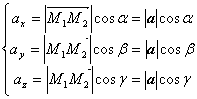，当时，有

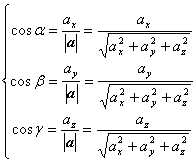
◆ 任意向量的方向余弦有性质：

◆ 与非零向量a同方向的单位向量为：

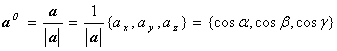
3． 例子：已知两点M₁(2,2,)、M₂(1,3,0)，计算向量的模、方向余弦、方向角以及与同向的单位向量.

解：＝{1-2，3-2，0-}={-1，1，-}

，，

，，

设为与同向的单位向量，由于

即得

小结：向量的坐标是本章向量代数的一个难点，是学好后继内容的基础，学生应多花时间学深学透.