第二节 数量积 向量积

教学目的：让学生搞清楚数量积与向量积的概念及其应用，掌握向量平行、垂直等重要的结论，为空间曲面等相关知识打好基础.

教学重点：1. 数量积、向量积的概念及其等价的表示形式

2.向量平行、垂直的应用

教学难点：1.活学活用数量积、向量积的各种形式

2.向量平行与垂直的相应结论

教学内容：

一．数量积：

● 定义：，式中为向量a与b的夹角.

● 物理上：物体在常力F作用下沿直线位移s，力F所作的功为

其中为F与s的夹角.

● 性质：Ⅰ.

Ⅱ.两个非零向量a与b垂直的充分必要条件为：

Ⅲ.

Ⅳ.

Ⅴ. 为数

● 几个等价公式：

Ⅰ.坐标表示式：设a = {a_x，a_y，a_z}，b = {b_x，b_y，b_z}则

Ⅱ.投影表示式：

Ⅲ.两向量夹角可以由式求解

● 例子：已知三点M(1,1,1)、A(2,2,1)和B(2,1,2)，求

提示：应用上求夹角的公式.

二．向量积：

● 概念：设向量c是由向量a与b按下列方式定义：

c的模，式中为向量a与b的夹角.

c的方向垂直与a与b的平面，指向按右手规则从a转向b.

※注意：数量积得到的是一个数值，而向量积得到的是向量.

● 公式：

● 性质：Ⅰ.

Ⅱ.两个非零向量a与b平行a∥b的充分必要条件为：

Ⅲ.

Ⅳ.

Ⅴ. 为数

● 几个等价公式：

Ⅰ.坐标表示式：设a = {a_x，a_y，a_z}，b = {b_x，b_y，b_z}则

Ⅱ.行列式表示式：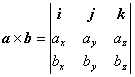

● 例子：已知三角形ABC的顶点分别为：A(1,2,3)、B(3,4,5)和C(2,4,7)，求三角形ABC的面积.

解：根据向量积的定义，

由于＝{2,2,2}，＝{1,2,4}

因此

于是

小结：本节是向量运算中很重要的部分，与上节共同讲述了向量的坐标表示以及向量的运算，这些是本章的一个重点.