第 五 节 隐函数的求导公式
教学目的:掌握由一个方程和方程组确定的隐函数求导公式,熟练计算隐函数的导函数。
教学重点:由一个方程确定的隐函数求导方法。
教学难点:隐函数的高阶导函数的计算。
教学内容:
一、一个方程的情形
在第二章第六节中我们已经提出了隐函数的概念,并且指出了不经过显化直接由方程
![]() =0
(1)
=0
(1)
求它所确定的隐函数的方法。现在介绍隐函数存在定理,并根据多元复合函数的求导法来导出隐函数的导数公式.
隐函数存在定理
1
设函数
![]() 在点
在点![]() 的某一邻域内具有连续的偏导数,且
的某一邻域内具有连续的偏导数,且![]() ,,
,, ![]() ,则方程
,则方程![]() =0在点
=0在点![]() 的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数
的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数![]() ,它满足条件
,它满足条件![]() ,并有
,并有
![]() (2)
公式(2)就是隐函数的求导公式
(2)
公式(2)就是隐函数的求导公式
这个定理我们不证。现仅就公式(2)作如下推导。
将方程(1)所确定的函数![]() 代入,得恒等式
代入,得恒等式
![]() ,
,
其左端可以看作是![]() 的一个复合函数,求这个函数的全导数,由于恒等式两端求导后仍然恒等,即得
的一个复合函数,求这个函数的全导数,由于恒等式两端求导后仍然恒等,即得
![]()
由于![]() 连续,且
连续,且![]() ,所以存在(x0,y0)的一个邻域,在这个邻域内
,所以存在(x0,y0)的一个邻域,在这个邻域内![]() ,于是得
,于是得
![]()
如果![]() 的二阶偏导数也都连续,我们可以把等式(2)的两端看作
的二阶偏导数也都连续,我们可以把等式(2)的两端看作![]() 的复合函数而再一次求导,即得
的复合函数而再一次求导,即得
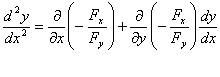
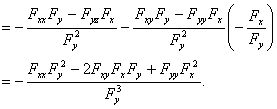
![]() 例1 验证方程
例1 验证方程![]() 在点(0,1)的某一邻域内能唯一确定一个单值且有连续导数、当
在点(0,1)的某一邻域内能唯一确定一个单值且有连续导数、当![]() =0时,
=0时,![]() 的隐函数
的隐函数![]() ,并求这函数的一阶和二阶导数在
,并求这函数的一阶和二阶导数在![]() =0的值。
=0的值。
解 设![]()
![]() ,则
,则![]() ,
,![]() .因此由定理1可知,方程
.因此由定理1可知,方程![]() 在点(0,1)的某邻域内能唯一确定一个单值且有连续导数、当
在点(0,1)的某邻域内能唯一确定一个单值且有连续导数、当![]() =0时,
=0时,![]() 的隐函数
的隐函数![]() 。
。
下面求这函数的一阶和二阶导数
![]() =
=![]() ,
, ![]() ;
;
![]() =
=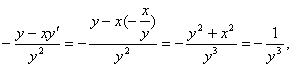
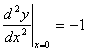 。
。
隐函数存在定理还可以推广到多元函数.既然一个二元方程(1)可以确定一个一元隐函数,那末一个三元方程
![]() (
(![]() )=0 (3)
)=0 (3)
就有可能确定一个二元隐函数。
与定理1一样,我们同样可以由三元函数![]() (
(![]() )的性质来断定由方程
)的性质来断定由方程![]() (
(![]() )=0所确定的二元函数
)=0所确定的二元函数![]() =
=![]() 的存在,以及这个函数的性质。这就是下面的定理。
的存在,以及这个函数的性质。这就是下面的定理。
隐函数存在定理2 设函数![]() (
(![]() )在点
)在点![]() 的某一邻域内具有连续的偏导数,且
的某一邻域内具有连续的偏导数,且![]() ,
,![]() ,则方程
,则方程![]() (
(![]() )=0在点
)=0在点![]() 的某一邻域内恒能唯一确定一个单值连续且具有连续偏导数的函数
的某一邻域内恒能唯一确定一个单值连续且具有连续偏导数的函数![]() ,它满足条件
,它满足条件![]() ,并有
,并有
![]() =
=![]() ,
,![]() =
=![]() .
(4)
.
(4)
这个定理我们不证.与定理1类似,仅就公式(4)作如下推导.
由于
![]() (
(![]() ,
, ![]()
![]() )≡0,
)≡0,
将上式两端分别对![]() 和
和![]() 求导,应用复合函数求导法则得
求导,应用复合函数求导法则得
![]() +
+![]()
![]() =0,
=0, ![]() +
+![]()
![]() =0。
=0。
因为![]() 连续,且
连续,且![]() ,所以存在点
,所以存在点![]() 的一个邻域,在这个邻域内
的一个邻域,在这个邻域内![]() ≠0,于是得
≠0,于是得
![]() =
=![]() ,
,![]() =
=![]() 。
。
例2
设![]() ,求
,求![]()
解 设![]() (
(![]() ) =
) =![]() ,则
,则![]() =2
=2![]() ,
, ![]() =
=![]() .应用公式(4),得
.应用公式(4),得
![]() =
=![]() 。
。
再一次![]() 对求偏导数,得
对求偏导数,得
![]()
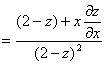
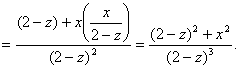
二、方程组的情形
下面我们将隐函数存在定理作另一方面的推广。我们不仅增加方程中变量的个数。而且增加方程的个数,例如,考虑方程组
![]() (5)
(5)
这时,在四个变量中,一般只能有两个变量独立变化,因此方程组(5)就有可能确定两个二元函数。在这种情形下,我们可以由函数![]() 、
、![]() 的性质来断定由方程组(5)所确定的两个二元函数的存在,以及它们的性质。我们有下面的定理。
的性质来断定由方程组(5)所确定的两个二元函数的存在,以及它们的性质。我们有下面的定理。
隐函数存在定理3 设函数![]() 、
、![]() 在点
在点![]() 的某一邻域内具有对各个变量的连续偏导数,又
的某一邻域内具有对各个变量的连续偏导数,又![]() ,
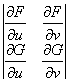
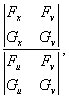
,![]() ,且偏导数所组成的函数行列式(或称雅可比(Jacobi)式):
,且偏导数所组成的函数行列式(或称雅可比(Jacobi)式):
![]()
![]() =
=
在点![]() 不等于零,则方程组
不等于零,则方程组![]() ,
,![]() 在点
在点![]() 的某一邻域内恒能唯一确定一组单值连续且具有连续偏导数的函数
的某一邻域内恒能唯一确定一组单值连续且具有连续偏导数的函数![]() ,它满足条件
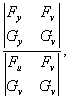
,它满足条件![]() ,并有
,并有
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
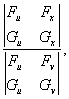 (6)
(6)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
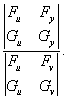
这个定理我们不证.
例3
设![]() ,求
,求![]() ,
,![]() ,
,![]() 和
和![]() .
.
解 此题可直接利用公式(6),但也可依照推导公式(6)的方法来求解。下面我们利用后一种方法来做。
将所给方程的两边对![]() 求导并移项,得
求导并移项,得
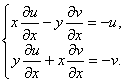
在![]() 的条件下,
的条件下,
![]()
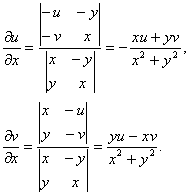
将所给方程的两边对![]() 求导,用同样方法在
求导,用同样方法在![]() 的条件下可得
的条件下可得
![]()
![]()
小结:
本节在前面已提出隐函数概念的基础上,根据多元复合函数的求导法导出隐函数的求导公式,给出了隐函数存在定理1、2、3,使我们能够计算有一个方程或方程组确定的隐函数的导数。