第八节 多元函数的极值及其求法
教学目的：了解多元函数极值的定义，熟练掌握多元函数无条件极值存在的判定方法、求极值方法，并能够解决实际问题。熟练使用拉格朗日乘数法求条件极值。
教学重点：多元函数极值的求法。
教学难点：利用拉格朗日乘数法求条件极值。
教学内容：
一、 多元函数的极值及最大值、最小值
定义 设函数
在点
的某个邻域内有定义，对于该邻域内异于的点，如果都适合不等式
，
则称函数
在点有极大值
。如果都适合不等式
，
则称函数在点有极小值
．极大值、极小值统称为极值。使函数取得极值的点称为极值点。
例1 函数
在点（0，0）处有极小值。因为对于点（0，0）的任一邻域内异于(0，0)的点，函数值都为正，而在点（0，0）处的函数值为零。从几何上看这是显然的，因为点（0，0，0）是开口朝上的椭圆抛物面的顶点。
例２ 函数
在点（0，0）处有极大值。因为在点（0，0）处函数值为零，而对于点（0，0）的任一邻域内异于（0，0）的点，函数值都为负，点（0，0，0）是位于
平面下方的锥面的顶点。
例３ 函数
在点（0，0）处既不取得极大值也不取得极小值。因为在点（0，0）处的函数值为零，而在点（0，0）的任一邻域内，总有使函数值为正的点，也有使函数值为负的点。
定理1（必要条件） 设函数在点具有偏导数，且在点处有极值，则它在该点的偏导数必然为零：
证 不妨设在点处有极大值。依极大值的定义，在点的某邻域内异于的点都适合不等式
特殊地，在该邻域内取
，而
的点，也应适合不等式
这表明一元函数
在
处取得极大值，因此必有
类似地可证
从几何上看，这时如果曲面在点
处有切平面，则切平面
成为平行于坐标面的平面
。
仿照一元函数，凡是能使
同时成立的点称为函数的驻点，从定理1可知，具有偏导数的函数的极值点必定是驻点。但是函数的驻点不一定是极值点，例如，点（0，0）是函数的驻点，但是函数在该点并无极值。
怎样判定一个驻点是否是极值点呢 ？下面的定理回答了这个问题。
定理2（充分条件） 设函数在点的某邻域内连续且有一阶及二阶连续偏导数，又，令
则在处是否取得极值的条件如下：
(1)
时具有极值，且当
时有极大值，当
时有极小值；
(2)
时没有极值；
(3)
时可能有极值，也可能没有极值，还需另作讨论。
这个定理现在不证。利用定理1、2，我们把具有二阶连续偏导数的函数的极值的求法叙述如下：
第一步 解方程组
求得一切实数解，即可以得到一切驻点。
第二步 对于每一个驻点，求出二阶偏导数的值
，
和
。
第三步 定出
的符号，按定理2的结论判定是否是极值、是极大值还是极小值。
例1 求函数
的极值。
解 先解方程组
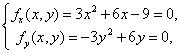
求得驻点为（1,0）、（1,2）、（-3,0）、（-3,2）。
再求出二阶偏导数
在点(1,0) 处，
又，所以函数在
处有极小值
；
在点(1,2) 处，
，所以(1,2)不是极值；
在点(-3,0) 处，
，所以(-3,0)不是极值；
在点(-3,2) 处，
又所以函数在(-3,2)处有极大值(-3,2)=31。
例2 某厂要用铁板作成一个体积为
解 设水箱的长为
，宽为
，则其高应为
，此水箱所用材料的面积
，
即 
（
，
）
可见材料面积是
和
的二元函数，这就是目标函数，下面求使这函数取得最小值的点
。
令
，
解这方程组，得：
，
从这个例子还可看出，在体积一定的长方体中，以立方体的表面积为最小。
二、条件极值 拉格朗日乘数法
拉格朗日乘数法 要找函数在附加条件
下的可能极值点，可以先构成辅助函数
其中
为某一常数求其对与的一阶偏导数，并使之为零，然后与方程(2)联立
（1）
由这方程组解出，及，则其中，就是函数在附加条件下的可能极值点的坐标。
这方法还可以推广到自变量多于两个而条件多于一个的情形。例如，要求函数
在附加条件
，
(2)
下的极值，可以先构成辅助函数
其中
，
均为常数，求其一阶偏导数，并使之为零，然后与(2)中的两个方程联立起来求解，这样得出的
就是函数
在附加条件(2)下的可能极值点的坐标。
至于如何确定所求得的点是否极值点，在实际问题中往往可根据问题本身的性质来判定。
例3 求表面积为
而体积为最大的长方体的体积。
解 设长方体的三棱长为
， 则问题就是在条件
（3）
下，求函数
的最大值。构成辅助函数
求其对
、z的偏导数，并使之为零，得到
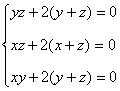（4）
再与(10)联立求解。
因、
都不等于零，所以由(11)可得
＝
， 
＝
．
由以上两式解得
将此代入式(10)，便得
=
这是唯一可能的极值点。因为由问题本身可知最大值一定存在，所以最大值就在这个可能的极值点处取得。也就是说，表面积为的长方体中，以棱长为的正方体的体积为最大，最大体积
。
小结：
本节以一元函数极值为基础，研究多元函数的最大值、最小值与极大值、极小值问题。在介绍多元函数极值的定义后，介绍了二元极值的性质以及利用偏导数求极值的步骤，讨论了二元函数的最值问题和实际问题的最值问题。最后介绍了利用拉格朗日乘数法求条件极值的方法及应用。