第四节 对面积的曲面积分

教学目的：理解和掌握对面积的曲面积分的概念性质及计算

教学重点：对面积的曲面积分的计算

教学难点：对面积的曲面积分的计算

教学内容：

一、对面积的曲面积分的概念与性质

1．空间曲面质量

在对平面曲线弧长的曲线积分中，将曲线换为曲面，线密度换为面密度，二元函数换为三元函数即可得对面积的曲面积分.设有一曲面.其上不均匀分布着面密度为上的连续函数，求曲面的质量.经分割，代替，求和，取极限四步，

2．定义

设曲面是光滑的，在上有界，把分成小块，任取，作乘积，再作和，当各小块曲面直径的最大值时，这和的极限存在，则称此极限为在上对面积的曲面积分或第一类曲面，记，即

=

说明：（1）为封闭曲面上的第一类曲面积分

（2）当连续时， 存在

（3）当为光滑曲面的密度函数时，质量

（4）=1时，为曲面面积

（5）性质同第一类曲线积分

（6）若为有向曲面，则与的方向无关.

二、对面积的曲面积分的计算方法

定理：设曲面的方程，在面的投影，若在上具有一阶连续偏导数，在上连续，则=

说明：（1）设为单值函数

（2）若：或可得到相应的计算公式.

（3）若为平面里与坐标面平行或重合时=

例1． 计算，为立体的边界

解：设，为锥面，

为上部分，

在面投影为

=，

∴+

=

=

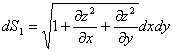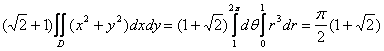
例2． 计算，由，，，的边界

解：

：，：，：，：

由对称性==

=.

==

==

∴原式==）+（）+（）=

例3． 计算，为被平面所割得部分

解：设第一象限内的部分为：，，

==

=

=

=

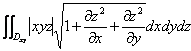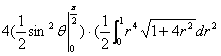
或

==

==

练习：，4，5，6，

小结：（1）对面积的曲线积分的概念和性质

（2）对面积的曲线积分的计算