从有限向无穷发展,在数学上是一种自然的趋势。无穷级数就是这一趋势的产物。

无穷级数是数学分析的一个重要工具，本章先将常数项级数，然后研究函数项级数，最后研究把函数展开为函数项级数的问题，我们只介绍两种最常用的级数展开式——泰勒级数展开式和付立叶级数展开式。

第一节 常数项级数的概念和性质

教学目的：理解常数项级数收敛、发散以及收敛级数的和的概念，掌握级数的基本性质及收敛的必要条件

教学重点：级数收敛与发散概念

教学难点：用级数收敛性及基本性质判别一些级数的收敛性问题

教学内容：

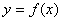
一、常数项级数的概念

1． 引入

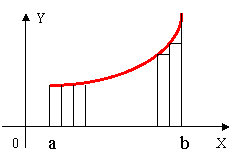
如图求曲边梯形的面积，可以表示成个内接矩形的面积的

和的极限；有：

一般地，有下面定义：

2．定义： 设已给序列：

数学式子 或记为，称为无穷级数，简称级数，其中叫做级数的通项，或一般项。

注：（1）各项都是常数的级数叫做常数项级数，如，等。

（2）各项是函数的级数，称为函数项级数，如，等。

（3）作常数项级数的前项的和，称为级数的部分和。从而的一个新的序列：，，，

3.定义：如果级数 的部分和数列有极限，即，则称级数收敛，这时极限叫做这级数的和，记为

注：（1）如果没有极限，则称级数发散。

（2）此时称为级数第项以后的余项。

例 1. 判断下列级数的敛散性:

解: (1)

故 即 收敛, 且.

(2)

故 即级数发散.

例 2. 证明等比级数（几何级数）当时收敛，当时发散。

证明：当时其前项和

若，则，于是，即当时等比级数收敛，且其和为。当，则。时，是无穷大量，级数发散。

若，则级数成为，于是，级数发散。

若，则级数成为，当为奇数时，，而当为偶数时，。当时，无极限，所以级数也发散。

二、收敛级数的基本性质

由级数收敛性定义，可得下面性质

性质1若级数收敛，其和为，又为常数，则也收敛，且

（级数的每一项同乘一个不为零的常数后，它的收敛性不回改变。）

性质2 若已知二收敛，则

（两个收敛级数可以逐项相加与逐项相减）

性质3 改变级数的有限项的值不改变级数的敛散性

性质4 收敛级数中的各项（按其原来的次序）任意合并（即加上括号）以后所成的新级数仍然收敛，而且其和不变。

推论 一个级数如果添加括号后所成的新级数发散，那么原级数一定发散。

注：例如 是收敛的，但级数发散。

性质5.级数收敛的必要条件: 若级数收敛，则

证明： 设，即，则，所以

推论 若级数的通项，当时不趋于零，则此级数必发散。

小结：本节主要是依据级数的定义及其性质判别级数的敛散性。如

⑴

∴级数发散

⑵

级数为，分别为等比级数且

∴原级数收敛

⑶

不趋于零 ∴原级数发散