第三节 幂级数
教学目的:了解幂级数的收敛域的构造及求法,如何将函数展开成幂级数,寒暑的幂级数展开式的应用。
教学重点:幂级数收敛域的求法,函数展开成幂级数的充要条件。
教学难点:幂级数收敛半径的求法,函数展开成幂级数的间接方法,近世计算中的误差估计
教学内容:
如果级数![]() 的各项都是定义在某区间
的各项都是定义在某区间![]() 中的函数,就叫做函数项级数。当自变量
中的函数,就叫做函数项级数。当自变量![]() 取特定值,如
取特定值,如![]() 时,级数变成一个数项级数
时,级数变成一个数项级数![]() 。如果这个数项级数收敛,称为
。如果这个数项级数收敛,称为![]() 函数项级数
函数项级数![]() 的收敛点,如发散,称
的收敛点,如发散,称![]() 为发散点, 一个函数项级数的收敛点的全体构成它的收敛域。
为发散点, 一个函数项级数的收敛点的全体构成它的收敛域。
一、幂级数的收敛域
1. 形如![]() 的幂级数
的幂级数
从简单的一个幂级数![]() 公比为
公比为![]() 的等比级数,当
的等比级数,当![]() 时收敛;当
时收敛;当![]() 时发散出发,因为它的收敛域是以0为中心,半径为1的对称区间,引课到
时发散出发,因为它的收敛域是以0为中心,半径为1的对称区间,引课到![]() 收敛域构造的阿贝尔定理:
收敛域构造的阿贝尔定理:
若有![]() 使
使![]() 收敛,则当
收敛,则当![]() 时,幂级数
时,幂级数![]() 绝对收敛;若有
绝对收敛;若有![]() 使
使![]() 发散,则当
发散,则当![]() 时,幂级数
时,幂级数![]() 发散。
发散。
定理 1. (Cauchy-Hadamard)
对冪级数![]() , 总存在非负数
, 总存在非负数![]() , 使其在
, 使其在![]() 内绝对收敛, 在
内绝对收敛, 在![]() 内发散.
内发散.
因此关于收敛半径的求法有如下定理:
已给幂级数![]() ,设当
,设当![]() 充分大以后都有
充分大以后都有![]() ,且
,且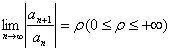 ,则: ⑴当
,则: ⑴当![]() 时,
时,![]()
⑵当![]() 时,
时,![]()
⑶当![]() 时,
时,![]()
例 1:求下列各幂级数的收敛域
⑴![]()
∵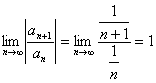 ∴
∴![]()
当![]() 时,级数成为
时,级数成为![]() (发散)
(发散)
当![]() 时,级数成为
时,级数成为![]() (收敛)
(收敛)
∴收敛域为![]()
⑵![]()
∵级数中只出现![]() 的偶次幂,缺项. ∴不能直接用定理来求
的偶次幂,缺项. ∴不能直接用定理来求![]()
可设![]() ,由比值法
,由比值法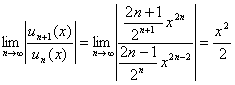
可知当![]() ,即
,即![]() ,幂级数绝对收敛
,幂级数绝对收敛
当![]() ,即
,即![]() ,幂级数发散,故
,幂级数发散,故![]()
当![]() 时,级数成为
时,级数成为![]() ,它是发散的,因此该幂级数的收敛域是
,它是发散的,因此该幂级数的收敛域是![]()
幂级数一般形式![]() 的讨论,可用变换
的讨论,可用变换![]() ,使之成为
,使之成为![]() 进行。
进行。
二、幂级数的运算
设幂级数
a0+a1x+a2x2+…+anxn+…
及
b0+b1x+b2x2+…+bnxn+…
分别在区间(-R,R)及(-R′,R′)内收敛,对于这两个幂级数,有下列四则运算:
加减法:
(a0+a1x+a2x2+…+anxn+…)±(b0+b1x+b2x2+…+bnxn+…)
=(a0± b0)+(a1± b1)x+( a2±b2)x2+…+(an±bn) xn+…
乘法:
(a0+a1x+a2x2+…+anxn+…)×(b0+b1x+b2x2+…+bnxn+…)
= a0 b0+( a0 b1+ a1 b0)x+( a0 b2+ a1 b1+ a2 b0) x2+…
+( a0 bn +a1 bn-1 +…+an b0) xn+…
可以证明上2式在(-R,R)与(-R′,R′)中较小的区间内成立.所以有:
定理 设![]() ,
, ![]() 的收敛域分别为
的收敛域分别为![]() , 则
, 则
(1) ![]()
(2) ![]()
幂级数的和函数有下列重要性质:
性质1 幂级数![]() 的和函数s(x)在其收敛域I上连续.
的和函数s(x)在其收敛域I上连续.
性质2 幂级数![]() 的和函数s(x)在其收敛域I上可积,并有逐项积分公式
的和函数s(x)在其收敛域I上可积,并有逐项积分公式
![]()
逐项积分后所得到的幂级数和原级数有相同的收敛半径.
性质3 幂级数![]() 的和函数s(x)在其收敛区间(-R,R)内可导,且有逐项求导公式
的和函数s(x)在其收敛区间(-R,R)内可导,且有逐项求导公式
![]()
逐项求导后所得到的幂级数和原级数有相同的收敛半径.
例2: 求幂级数![]() 的和函数.
的和函数.
解 先求收敛域.由![]() 得收敛半径R=1.
得收敛半径R=1.
在端点x=-1处,幂级数成为![]() ,是收敛的交错级数;
,是收敛的交错级数;
在端点x=1处,幂级数成为![]() ,是发散的.因此收敛域为I=[-1,1].
,是发散的.因此收敛域为I=[-1,1].
设和函数为s(x),即![]() 于是
于是![]()
利用性质3,逐项求导,并由![]()
得![]()
对上式从0到x积分,得![]()
于是,当![]() 时,有
时,有![]()
而s(0)可由s(0)=a0=1得出,
故