第四节 函数展开成幂级数

教学目的：了解如何将函数展开成幂级数

教学重点：幂级数收敛域的求法，函数展开成幂级数的充要条件。

教学难点：函数展开成幂级数的间接方法

教学内容：

定理：设函数在点的某一邻域内只有各阶导数，则在该邻域内能展开成Taylor级数的充分条件是的Taylor公式中的余项当时的极限为零。

取时，称为函数的麦克劳林级数

函数展开成幂级数的方法

1．直接方法：

（1）求的各阶导数

（2）求

（3）写出幂级数，且求出

（4）考察余项是否趋于零？如趋于零，则在内的幂级数展开式为

例如， 可用此法分别求出和的展开式：

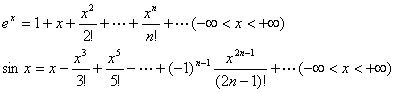
2．间接方法：利用幂级数可以逐项求导，逐项积分进行

例如，

注:必须熟记五个函数的幂级数展开式：

例3 将函数展开成（x-1）的幂级数

解 因为

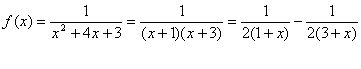
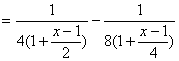
而

， （）

（）

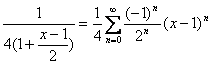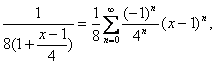所以

， （）

小结：

幂级数是函数项级数中最基本的一类。它的特点是在其收敛区间绝对收敛，且幂级数在收敛区间内可逐项微分和积分。由此第一次得到了一种函数的无限形式的表达式（即幂级数展开式），将函数展为幂级数无论在理论研究方面还是在应用方面都有着重大的意义。

一个函数的幂级数展开式只依赖函数在展开点出的各阶导数，这是Taylor级数的优点。但从另一方面看，这又是它的缺点，因为求任意阶导数并不容易，而且许多函数难以满足这样强的条件。还应看到，若想取级数的前项和作为函数的近似值，则在离开展开点稍远一点的地方，取非常大才能使误差在所要求的限度内。