第四节 一阶线性微分方程

教学目的：掌握一阶线性微分方程的形式，熟练掌握其解法；掌握利用变量代换解微分方程的方法；了解贝努里方程的形式及解法

教学重点：一阶线性微分方程的形式,及解的形式，利用变量代换解微分方程

教学难点：一阶线性微分方程通解的形式，利用变量代换解微分方程

教学内容：

一、一阶线性方程

1、定义 方程 （1）称为一阶线性微分方程。

特点 关于未知函数及其导数是一次的。

若，称（1）为齐次的；

若，称（1）为非齐次的。

如：（1） （2）

2、解法

当时，方程（1）为可分离变量的微分方程。

当时，为求其解首先把换为0，即

（2）

称为对应于（1）的齐次微分方程，求得其解

为求（1）的解，利用常数变易法，用代替，即

于是，

代入（1），得

故 。 （3）

3、例1 求方程

（4）

的通解.

解 这是一个非齐次线性方程。先求对应的齐次方程的通解。

，

，

，

（5）

用常数变易法。把换成，即令

，

则有 ，

代入（1）式中得

，

两端积分，得 。

再代入（4）式即得所求方程通解

。

方法二、 我们可以直接应用（3）式

得到方程的通解，其中，

，

代入积分同样可得方程通解

，

此法较为简便，因此，以后的解方程中，可以直接应用（3）式求解。

二、Bernoulli方程

1、定义 称为贝努里方程。

当时，为一阶线性微分方程。

2、解法 两边同除

令，则有

而

为一阶线性微分方程，故

。

贝努里方程的解题步骤

（1） 两端同

（2） 代换

（3） 解关于的线性微分方程

（4） 还原

例2 设可微函数满足方程

求.

解, 将方程两边对求导数得

,

即 ,

此为贝努里方程.

用除方程两边

令, 则有

,

故, .

代入得: .

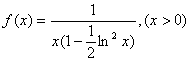3. 利用变量代换解微分方程

例3 解方程

解 令 ，则 ，于是

解得 ， 即

例4 解方程

解 令则代入原方程，得

。

分离变量得

两端积分得 。

以代入上式，即得

或

小结：本节讲述了一阶线性微分方程，及贝努力方程的解法，利用常数变易法，和变量代换法来解微分方程。

作业：《高等数学（同济5）》第282页 1、2、3、6、9题