第五节、全微分方程

教学目的：掌握全微分方程成立的充要条件，掌握全微分方程的解法，会用观察法找积分因子

教学重点：全微分方程的解法，观察法找积分因子

教学难点：全微分方程的解法，观察法找积分因子

教学内容：

1． 定义

若 （1）

恰为某一个函数的全微分方程，即存在某个，使有，则称（1）为全微分方程。

可以证明 是（1）式的隐式通解。

2．解法 若，在单连通域G内具有一阶连续偏导数，条件

是（1）式为全微分方程的充要要条件。

通解为 。

例1 求解

解 令 ，

则

此方程为全微分方程。于是

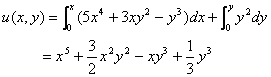
通解为

3．积分因子

若，则（1）式不是全微分方程，但若有一个适当函数，使（1）式乘以后为全微分方程，称函数为积分因子。

一般积分因子不好求，我们只要求通过观察找到积分因子。

例2 方程 不是全微分方程，但

于是将方程乘以 ，则有 ，

即 ，从而为其通解。此时为其积分因子。

注意 积分因子一般不唯一。

如上述方程，若同乘有 ，

于是 ，即 为其通解。 也是其积分因子。

小结：

1．本节讲述了一阶线性微分方程，及贝努利方程的解法，利用常数变易法，和变量代换法来解微分方程。

2．本节讲述了全微分方程的解法，用观察法找积分因子，使之满足全微分方程的充要条件。