3.2 曲线的凹凸性与拐点

l 教学目标与要求

通过学习，使学生掌握利用二阶导数的符号判定函数在某一区间上凹凸性的方法，为更好地描绘函数图形打好基础，同时，理解拐点的定义和意义。

教学重点：利用函数的二阶导数判断曲线的凹凸性与拐点。

教学难点：理解拐点的定义和意义。

证明曲线凹凸性判定定理时，除了利用“拉格朗日中值定理”证明外，还可用“泰勒定理”来证明；如果利用“拉格朗日中值定理”证明，则要配合函数图形来分析讲解如何想到需要两次使用“拉格朗日中值定理”的思路，切忌脱离图形，机械证明，让学生领悟不到思想，摸不着头脑。

在讲函数的凹凸性和曲线拐点的定义时，要强调凹凸性并不是曲线的固有性质，而是函数的性质，与所选的坐标系有关；而拐点是曲线的固有性质，与所选的坐标系无关。

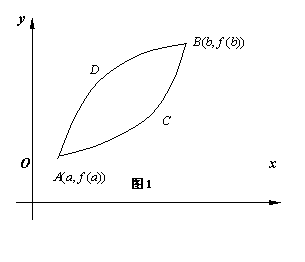函数的单调性对于描绘函数图形有很大作用，但仅仅由单调性还不能准确描绘出函数的图形。比如，如果在区间上，，则我们知道在区间上单调增，但作图（参见图1）的时候，我们不能判断它增加的方式（是弧，还是弧），即不能判断曲线的凹凸性，所以研究曲线的凹凸性对于把握函数的性态、作图等是很有必要的！

在图1中，对于上凸的曲线弧，取其上任意两点，不妨取作割线，我们总会发现不论两点的位置，割线段总位于弧段的下方，这种位置关系可以用不等式

来描述。同理，对于上凹的曲线弧，总可用不等式

来描述。由此，我们想到对曲线的凹凸性做如下定义：

凹凸性定义设在区间I上连续，如果对I上任意两点，，恒有

则称在I上的图形是（向上）凹的，简称为凹弧；如果恒有

则称在I上的图形是（向上）凸的，或简称为凸弧。

如果沿曲线从左向右走，则图形是（向上）凸的曲线的几何意义相当于右转弯，图形是（向上）凹的曲线相当于左转弯，而有切线的凹凸弧的分界点正是曲线转向的点，我们把这样的点称为拐点。

曲线凹凸性的定义自然能判别曲线的凹凸性，但实际使用起来需要取两个点，且两个不等式对于一些表达式较复杂的函数来说判断起来也不容易。因此，我们就想能否用其它方法来判定曲线的凹凸性。函数的单调性能由的符号确定，而对于凹凸性它束手无策，所以我们猜想凹凸性是否和有关？

经过分析，并利用泰勒公式，可证实我们的猜想是正确的，函数图形的凹凸性的确和的符号有关,于是得到了判断曲线凹凸性的定理。

定理设在上连续, 在内具有二阶连续导数,那么：

（1）若在内>0，则在上的图形是凹的；

（2）若在内<0，则在上的图形是凸的。

例讨论函数

的性态，并指出有关性质。

解定义域为∪

分界点

分界点，作表如下

结论：单增区间：，单减区间：

上凸区间：，上凹区间：，拐点：

极大值：，渐近线：