5.2 微积分基本定理
（翟美娟 王军秋）
l
教学目标与要求
充分理解并会初步使用牛顿—莱布尼兹公式，对变上限函数会求导。
l
教学重点与难点
教学重点：牛顿—莱布尼兹公式。
教学难点：积分上限函数的概念及其导数。
l
教学方法与建议
定积分的概念是从实际问题提出的，然而却面临着计算复杂的问题，这是一个必须解决的问题。首先
通过变速直线运动问题，引出定积分计算公式—当然这是一猜想；再通过积分上限函数的导数的基本公式，证明了该猜想即牛顿—莱布尼兹公式。体现了实践—理论—再实践的辩证法思想。
l
教学过程设计
1．问题提出
考虑 变速直线运动中位置函数与速度函数的联系
设某物体作直线运动，已知速度
是时间间隔
上
的一个连续函数，且
，求物体在这段时间内所经过的路程.变速直线运动中路程为
另一方面这段路程可表示为
，
所以
这个由特殊问题得出来的关系，是否具有一般性呢？回答是肯定的。为此引入：
2．积分上限函数及其导数
设函数
在区间
上连续，当
在区间上任意取定一个值时，定积分
有一个对应值，所以它在上定义了一个函数，记为
称为积分上限函数.积分上限函数有性质：
定理１ 如果在上连续，则积分上限的函数
在上具有导数，且它的导数是
其中
证 由定义
由积分中值定理得
，其中
由于的连续性，
补充：设
则
=
如果
连续，
、
可导，则
的导数为
例1 求极限
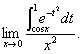
解 这是0/0型不定式，应用洛必达法则.
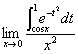
例2 设在
上连续，且
.证明
在上只有一个解.
证 令
所以
在上为单调增加函数.
所以由连续函数的介值定理知，
即原方程在上只有一个解.
定理2（原函数存在定理） 如果在上连续，则积分上限的函数
就是在上的一个原函数.
定理的重要意义：
（1）肯定了连续函数的原函数是存在的.
（2）初步揭示了积分学中的定积分与原函数之间的联系.
3．牛顿—莱布尼茨公式
定理 3（微积分基本公式）如果是连续函数在区间上的一个原函数，则
证 已知是的一个原函数，又
也是的一个原函数,
，令
，有
再由
该公式称为牛顿-莱布尼茨公式，或微积分基本公式。
微积分基本公式表明：
1) 一个连续函数在区间上的定积分等于它的任意一个原函数在区间上的增量.求定积分问题转化为求原函数的问题.
2) 本公式：
是微积分的核心！！他充分体现了数学的简洁之美！原本一个冗长且复杂的求和极限（定积分）问题，却和不定积分这样两个看起来相去甚远的问题，如此完美地结合在一起，犹如天造地设一般，令人叹为观止！
3) 牛顿，莱布尼茨二人创立微积分，牛顿在先，莱布尼茨在后，只因莱布尼兹采用的数学记号简洁！ 所以二人名字共用至今。
4)牛顿－莱布尼茨公式沟通了微分学与积分学之间的关系．
注意：当
时，
仍成立.
例3 求积分
解 利用牛顿－莱布尼茨公式
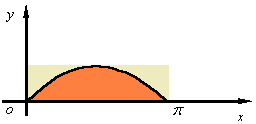例4 计算曲线
在
上与轴所围成的平面图形的面积.
解 面积为
