5.3 广义积分

（王 艳 陈 光）

l 教学目标与要求

能够正确理解广义积分的定义，会计算广义积分。

l 教学重点与难点

教学重点：广义积分的定义剖析，计算。

教学难点：广义积分敛散性的判断

l 教学方法与建议

从定积分出发，对进行推广。提出广义积分的概念，应特别弄清广义积分收敛的意义。教学关键是弄清广义积分收敛的概念。

l 教学过程设计

1. 无穷限的广义积分

我们在讨论黎曼函数积分时有两个最基本的约束：积分区间的有穷性和被积函数的有界性。但实际问题却突破了这些约束，需要考虑无穷区间上的积分或对无界函数求积分。于是便有了广义积分的概念，这也是我们这节课要学的内容。

定义1 设在上连续，,记

，

称之为上的无穷限的广义积分，若极限

存在，称广义积分收敛；若极限不存在，则称广义积分发散。

同理可定义

若广义积分

，

都收敛，则称广义积分

收敛，否则称之发散.

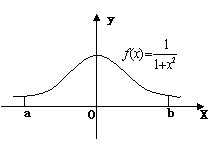
例1． 计算广义积分

解 由定义，有

=+

=

几何意义：函数下方图形的面积

2．无界函数的广义积分

定义2 (1)设在上连续,而在的右邻域内无界,取,记

=

称之为在上的广义积分(瑕积分),

例2 计算广义积分 .

解 因为

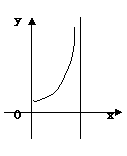所以被积函数在点的左邻域内无界，于是

==

几何意义：曲线

之下，轴之上，直线与之间的图形面积.