6.1 定积分应用
(王梦婷 徐裕生)
l 教学目标与要求
使用定积分的元素法来求解旋转体体积及旋转面面积。
l 教学重点与难点
教学重点:求旋转体体积及旋转面面积。
教学难点:旋转面面积公式的推导。
l 教学方法与建议
我们已经学习了定积分的元素法,知道在“划分,近似,求和,求极限”中最关键的一步是“近似”,而“近似”的关键就是“以直代曲,以常量代变量”。那么在求解旋转体体积及旋转面面积时一定要一直贯彻和强调这个思想。
l 教学过程设计
旋转体体积
一个平面图形绕在其平面内的一条直线旋转一周,就产生一个旋转体。
例如:圆柱体、圆锥体、圆台(如下图)。
在![]() 面内由连续曲线
面内由连续曲线![]() 及
及![]() 轴围成的平面图形A绕
轴围成的平面图形A绕![]() 轴得一旋转体,此旋转体体积被可分成一层一层的薄片,取
轴得一旋转体,此旋转体体积被可分成一层一层的薄片,取![]() 上微元
上微元![]() ,则有
,则有
![]()
从而
![]() 。
。
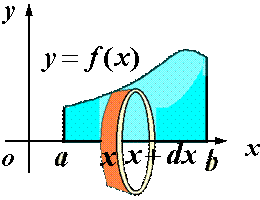 A绕
A绕![]() 轴也可得一旋转体,我们换一种分法,我们把它分成一层一层柱壳,同样地,在
轴也可得一旋转体,我们换一种分法,我们把它分成一层一层柱壳,同样地,在![]() 内任取一小区间
内任取一小区间![]() ,让其绕
,让其绕![]() 轴旋转,得一薄柱壳,内表面积为
轴旋转,得一薄柱壳,内表面积为![]() ,把它展开就得到一块近似于厚为
,把它展开就得到一块近似于厚为![]() ,面积为
,面积为![]() 的矩形薄板,从而得柱壳的体积元素
的矩形薄板,从而得柱壳的体积元素
![]()
从而
![]() 。
。
同样地,对于![]() 面内由连续曲线
面内由连续曲线
![]()
及![]() 轴所围平面图形B绕
轴所围平面图形B绕![]() 轴、
轴、![]() 轴所得旋转体体积也可求出来。
轴所得旋转体体积也可求出来。
2. 举例求旋转体体积
例: 求![]() 及
及![]() 轴所围图形分别绕
轴所围图形分别绕![]() 轴、
轴、![]() 轴所得旋转体体积。
轴所得旋转体体积。