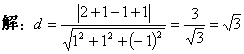7.2 平面及其方程

（权豫西 李琪）

l 教学目标与要求

会求平面的方程，进而加深对数量积和向量积的认识

l 教学重点与难点

教学重点：建立平面的方程

教学难点：如何利用向量积的物理意义来建立平面的三点式方程和求解一些平面方程

l 教学方法与建议

在建立平面的三点式方程中，要利用图形和向量积的方向特点相结合来推导平面的法向量，从而利用点法式方程推出平面的三点式方程；对特殊的平面，应该通过做图让学生加深印象；对同一个问题尽量采用不同的解法，以开拓学生的解题思路。教学的关键是让学生知道两向量垂直从而数量积为零在平面方程建立中的作用。

l 教学过程设计

1. 问题提出与平面方程的建立

平面是空间曲面中最简单、特殊的一类，平面方程的建立将有助于我们理解第八章中关于“微分法在几何中的应用”以及“曲面积分”这一部分的内容，所以我们需要建立平面的方程。

平面的方程满足两个条件：

（1）平面上的点都满足方程（动点）

（2）满足方程的点都在平面上

1．平面的点法式方程

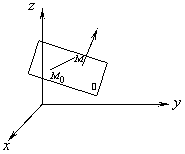过点且以为法向量的平面方程称为平面的点法式方程，向量就叫做该平面的法线向量。易知：平面上的任一向量均与该平面的法线向量垂直.

我们知道，过空间一点可以作而且只能作一平面垂直于一已知直线，所以当平面Ⅱ上一点和它的一个法线向量为已知时，平面Ⅱ的位置就完全确定了。这时平面方程为：

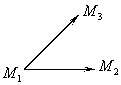
2．平面的三点式方程

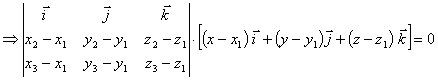
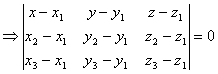
例１ 求过三点、、的平面π的方程。

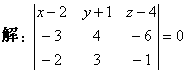
即

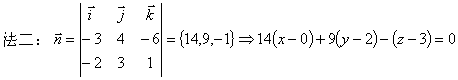
3．平面的一般方程

由平面的点法式方程与三点式方程可以发现，平面的方程都是三元一次方程。

反之，设有三元一次方程

⑴

我们任取满足该方程的一组数，，即：

⑵

把上述两式相减，得

⑶

把它与平面的点法式方程作比较， 可以知道方程⑶是通过点且以为法线向量的平面方程， 但方程⑴与⑶同解，这是因为由⑴—⑵即得⑶， 又由⑶加⑵就得⑴，由此可见，任一三元一次方程⑴的图形总是一个平面，方程⑴称为平面的一般方程，其中,,的系数就是该平面的一个法线向量的坐标，即

对于一些特殊的三元一次方程，应该熟悉它们的图形特点。

时，方程表示一个通过原点的平面；

时，方程，法线向量，它的轴上的投影为零，垂直于轴，方程表示一个平行于轴的平面。

和分别表示一个平行于轴和轴的平面。

时，方程,法线向量同时垂直轴和轴。方程表示一个平行于面的平面。

和分别表示一个平行于面和面的平面。

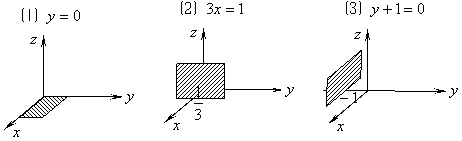
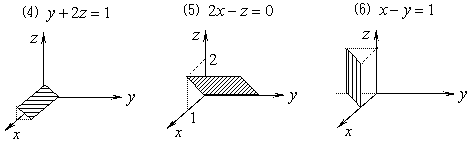
例２ 指出下列各方程所代表的图形特点，并画草图。

例３ 过通过轴和点的平面方程。

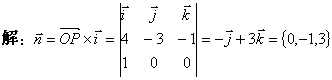
平面：，即

两平面的夹角（两平面的法线向量的夹角）（指锐角）

平面：

平面：

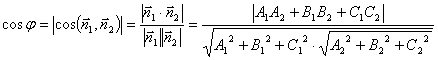
注:若分母为零时,理解分子同时为零

例４ 一平面通过两点和且垂直于平面，求它的方程.

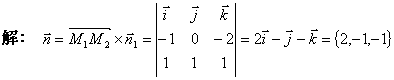
方程为

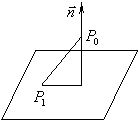
4．点到平面的距离公式

点到平面∏：的距离

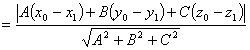
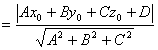
例５ 求点到的距离。