8.2 多元函数极值及其求法

（魏宗田 郭乔）

l 教学目的与要求

理解多元函数，尤其二元函数极值与最值的概念，掌握二元函数极值存在的充分与必要条件以及极值的求法。

l 教学重点与难点

教学重点：二元函数极值存在的充分与必要条件，求二元函数极值的方法与一般步骤。

教学难点：二元函数极值存在的充分条件。

l 教法分析

在优化问题中，往往会遇到求一定条件下某个量所能达到的最大或最小值。这类问题一般用数学的方法可以解决，即所谓函数的极值或最值问题。一元函数的极值求法学生已经掌握，二元函数极值问题是一元函数极值问题的推广，但情况要复杂得多。因此给出二元函数极值的概念时应多用实例说明，尽可能做到直观易懂。二元函数极值存在的必要与充分条件是建立极值求法的理论基础，主要使学生熟悉定理内容，充分性证明不作要求。掌握二元函数极值及某些实际问题最值的求法是重点，必须精心选则典型、难易适中的例子，使学生感兴趣、易掌握。

l 教学设计

1．问题提出与定义

由实际应用中产生的函数极值问题是高等数学的一个重要研究课题。我们已经掌握了一元函数极值的求法，但是由于实际问题的需要，我们必须考虑二元乃至多元函数的极值问题。请看下例

例1 要做一个体积为的有盖长方体水箱，问当长、宽、高各取多大时，才能使用料最省？

解 设长、宽分别为，则高为，水箱用料（即长方体表面积）为

。

由实际问题知，此二元函数必有极小值，但我们现在还不知道它的求法。为了解决此类问题，我们首先要给出二元函数极值的定义。与一元函数类似，我们可以用邻域定义之。

定义 设函数在点的某个邻域内有定义，如果对于该邻域内任一异于的点，都有，则称函数在点有极大值；在相同条件下，如果，则称函数在点有极小值。在上述情况下称为的极值点。

例如，函数 在点处有极小值，直观上看，是开口向上的椭圆抛物面。再例如，函数（锥面）在点处明显有极大值。而函数（马鞍面）在点不取极值，这可以从图像上看出。

元函数极值定义是二元函数极值定义的自然推广。设元函数在点的某邻域内有定义，如果对该邻域内异于的点都适合不等式，则称元函数在点有极大值（极小值）。

我们着重讨论二元函数极值。对于二元函数的极值，我们有函数取得极值的必要条件和充分条件。

2．二元函数极值的求法

假设二元函数具有二阶连续偏导数，则其极值求法如下：

第一步：解方程组

求出驻点；

第二步：对于每一个驻点，求出二阶偏导数的值和；

第三步：确定的符号,按照充分条件（定理2）判定驻点是否为极值点。

对偏导数不存在的点应一并考虑。

3．二元函数极值求法示例

例 求函数

的极值

解 函数处处存在二阶篇导数，故先解方程组

，

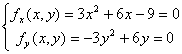得驻点为.计算结果由下表给出。

	(1, 0)	(1, 2)	(-3, 0)	(-3, 2)
	+	_	_	+
	+	非极值点	非极值点	_
	极小值			极大值

求得结果为极小值，极大值。