11.1 正项级数敛散性判别法

（侯筱婷 赵彦晖）

l 教学目标与要求

掌握正项级数敛散性的判别方法，为判定一般级数的敛散性打好基础。

l 教学重点与难点

教学重点：判别正项级数敛散性的比较审敛法和比值审敛法。

教学难点：理解调和级数发散的原因。理解比值审敛法失效的原因。

l 教学方法与建议

要给学生指出正项级数在发散时，一定发散到+∞.

要求学生记住几个典型的正项级数：

（1）等比级数：等比级数

在时收敛，q ≥1时发散。

（2）p级数：p级数

在p ＞1时收敛，p ≤1时发散。

应用比较审敛法判断一个正项级数敛散性时，要教给学生如何猜出或估计出正项级数的敛散性并寻找已知其敛散性的比较对象。找到了比较对象，就可以用已知敛散性的级数为参照，通过比较审敛法判断原级数是收敛的还是发散的。

l 教学过程设计

1．正项级数的概念

【定义】若级数

中各项都是非负的( 即)，则称该级数为正项级数。

由于许多级数的敛散性可归结为正项级数的敛散性，因此，正项级数的敛散性判定就显得十分重要。

2．正项级数收敛的充要条件

【充要条件】正项级数收敛的充要条件是它的部分和数列有界。

例1 证明调和级数

是发散的。

证 如图，由微分学知，当时，故调和级数的部分和

所以调和级数级数发散。

调和级数是一个很重要的发散级数。

借助正项级数收敛的充要条件，我们还可建立一系列具有实用性的正项级数审敛法。

3．基本审敛法

【比较审敛法】对正项级数

（1）如果，则有结论：

（2）如果极限

则当时两级数同敛散；如果极限为0，则

如果极限为，则

比较审敛法的实质是：

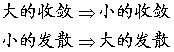
例2 判别下列级数的收敛性

解 由于

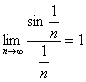
所以，由比较审敛法知此级数发散。

若取比较对象为

则可建立判别容易的比值审敛法和根值审敛法。

【比值、根值审敛法】若正项级数

适合

则当时级数收敛；当(也包括)时级数发散；当时无法判定。

例3 判别下列级数的收敛性

解 （1）由于极限

所以由根值审敛法知级数收敛。

（2）由于比值

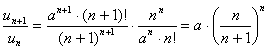
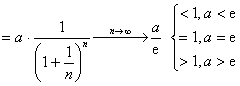
[注] 对于比值审敛法与根值审敛法失效的情形()，其级数的敛散性应另寻它法加以判定，通常是构造更精密的审敛法。一种比较简单的更精密的审敛法是

【比值放大判别法1】若正项级数

适合

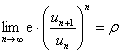
则当时，级数收敛；当(也包括)时，级数发散；当时，无法判定。

该判别法的证明见《西安建筑科技大学学报》（1999年第2期）“正项级数的比值放大判别法（赵彦晖）”。在该文中作者给出了一类（无穷多个）正项级数判别法，这些判别法中一个比一个更精密，在一个判别法失效时可换另一个更精密的判别法，甚至可以无限精密。

利用该文中最简单的一个审敛法（即上述比值放大审敛法1）即可判别例3（2）中比值审敛法失效的情形：这时有

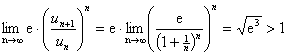
再如对p级数

比值审敛法与根值审敛法显然已失效，若用比值放大判别法1，则有
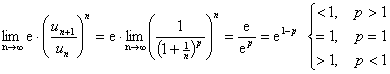