11.2 绝对收敛与条件收敛
（李阳 徐宗辉）
l 教学目标与要求
了解绝对收敛与条件收敛的定义、计算、区别。
l 教学重点与难点
教学重点：绝对收敛与条件收敛的计算。
教学难点：绝对收敛与条件收敛的区别。
l 教学方法与建议
重点区分绝对收敛与条件收敛的区别及他们判定方法的条件。教学关键是将课本中的性质细化，加强学生对概念定理的进一步理解与引用
l 教学过程设计
1．问题提出与定义
在以前的学习中我们了解到：对于无穷级数
如果此级数的部分和数列
有极限
，即
则称无穷级数（1）收敛，这时极限叫做这级数的和，并写成
如果没有极限，则称无穷级数（1）发散。
如果给无穷级数（1）的各项都加上绝对值，即
则它的的敛散情况怎样？可以证明，如果级数（2）收敛，则级数（1）必定收敛。
为此，我们引入
定义 如果级数（1）各项的绝对值所构成的正项级数（2）收敛，则称级数（1）绝对收敛；如果级数（1）收敛，而级数（2）发散，则称级数（1）条件收敛。
容易知道，级数
是绝对收敛，而级数
是条件收敛级数。
2．举例
例1 判别级数
的敛散性。
解 根据比较审敛法
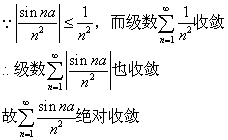
例2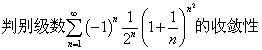 
解 根据根值审敛法
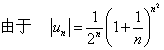
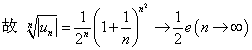
而
，因此级数发散。
4．绝对收敛级数性质
绝对收敛级数有很多性质是条件收敛级数所没有的，下面给出关于绝对收敛级数的两个性质。
定理 绝对收敛级数经改变项的位置后构成的级数也收敛，且与原级数有相同的和（即绝对收敛级数具有可交换性）