Gauss消元法(也称为顺序Gauss消元法)是一种古老的求解线性方程组的方法。其基本思想是在逐步消元的过程中,把系数矩阵约化成上三角矩阵,从而将原方程组约化为容易求解的等价三角方程组,再通过回代过程即可逐一求出各未知数。下面以四阶线性方程组为例来说明Gauss消元法的基本思想。
一 消元与回代
将线性方程组Ax=b逐步化为同解上三角形方程组A(n)x=b(n)的计算过程,称为消元过程,按方程相反顺序自下而上逐步求解方程组A(n)x=b(n),计算xn,xn-1,…,x2,x1的过程,叫做回代过程。
设 ,
,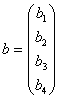 ,detA≠0,记Ax=b的增广矩阵为:(A,b)=(A(1),b(1))=
,detA≠0,记Ax=b的增广矩阵为:(A,b)=(A(1),b(1))=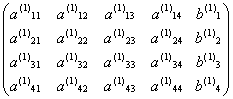
假定![]() ,第一步消元是从方程组的第2至4个方程中消去未知数
,第一步消元是从方程组的第2至4个方程中消去未知数![]() 。为此,对(A(1),b(1))做如下计算:
。为此,对(A(1),b(1))做如下计算:
l 计算行乘数![]()
2 第![]() 行元素减去第一行对应元素乘以
行元素减去第一行对应元素乘以![]() ,将(A(1),b(1))的第一列主对角元以下元素化为零,同时有:
,将(A(1),b(1))的第一列主对角元以下元素化为零,同时有:
![]()
![]()
![]()
![]()
将(A(1),b(1))化为如下形式,并记为(A(2),b(2)):
![]()
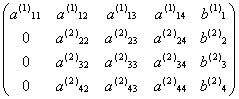
如果![]() ,因矩阵A非奇异,在A的第一列元素中至少有一个不为零,设
,因矩阵A非奇异,在A的第一列元素中至少有一个不为零,设![]() ,交换A的第1和第
,交换A的第1和第![]() 行后再消元,所得矩阵A(1)的右下角
行后再消元,所得矩阵A(1)的右下角![]() 阶矩阵也非奇异,否则会推出与detA≠0矛盾的结果。
阶矩阵也非奇异,否则会推出与detA≠0矛盾的结果。
第二步消元是从方程组的第3至4个方程中消去未知数![]() 。为此,对(A(2),b(2))做如下计算:
。为此,对(A(2),b(2))做如下计算:
l 计算行乘数![]()
2 第![]() 行元素减去第二行对应元素乘以
行元素减去第二行对应元素乘以![]() ,将(A(2),b(2))的第二列主对角元以下元素化为零,同时有:
,将(A(2),b(2))的第二列主对角元以下元素化为零,同时有:
![]()
![]()
![]()
![]()
将(A(2),b(2))化为如下形式,并记为(A(3),b(3)):
![]()
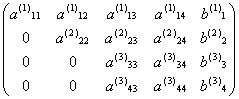
最后一步消元是从方程组的第4个方程中消去未知数![]() 。为此,对(A(3),b(3))做如下计算:
。为此,对(A(3),b(3))做如下计算:
l 计算行乘数![]()
2 第![]() 行元素减去第三行对应元素乘以
行元素减去第三行对应元素乘以![]() ,使(A(3),b(3))的元素
,使(A(3),b(3))的元素![]() 为零,同时有:
为零,同时有:![]() ,
,![]()
将(A(3),b(3))化为如下形式,并记为(A(4),b(4)):
![]()
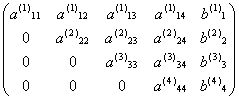
因为![]() ≠0,而
≠0,而![]() =
=![]() ,所以,
,所以,![]() ,(
,(![]() =1,2,3,4)。最后,解出上三角方程组
=1,2,3,4)。最后,解出上三角方程组![]() ,就得到原方程组
,就得到原方程组![]() 的解。
的解。
上述方法可推广到一般情况。对于n阶线性方程组,假定已完成k—1步消元,将(A(1),b(1))化为具有如下形式的(A(k),b(k)):
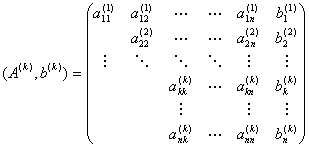
后可做如下计算:
1 计算行乘数![]()
2 第![]() 行(k+1
行(k+1![]() n)元素减去第k行对应元素乘以
n)元素减去第k行对应元素乘以![]() ,将(A(k),b(k))的第k列主对角元以下元素化为零,但
,将(A(k),b(k))的第k列主对角元以下元素化为零,但![]() 的值不为零,同时有:
的值不为零,同时有:
![]()
![]()
![]()
![]()
而(A(k),b(k))的前k行、k-1列都不变,即可将(A(k),b(k))化为上三角矩阵,记为(A(n),b(n)):
![]()
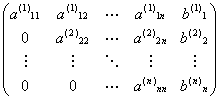
最后由回代公式: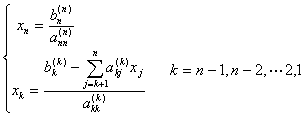
解出上三角方程组,即得出原方程组的解。
所以综上所述,如果矩阵A是非奇异矩阵,总可以通过带有行交换或不带行交换的消元过程,将A化为非奇异上三角形矩阵A(n),因此,回代求解过程也可以进行到底。但是,在实际应用中,常常难于事先判断系数矩阵A的奇异性,因此,需要进一步考虑当A为奇异矩阵时计算过程可能发生的情况。一是消元过程的某一步找不到非零主元素,于是计算中断;二是虽然消元过程能进行到底,但a(n)nn=0,使回代求解过程无法进行下去。因此,在算法设计中必须考虑到上述两种可能发生的情形,此时应在算法设计中给出计算中断的信息。
二 Gauss消元法的运算量
由于计算机完成一次乘(除)法花费的时间远超过做一次加(减)法的时间,而且按统计规律,在一个算法中,乘除法与加减法的运算次数大体相当,所以通常用所做乘除法的次数来衡量算法的运算量。
按公式在第![]() 步消元过程中,做乘法
步消元过程中,做乘法![]() 次,除法
次,除法![]() 次,完成
次,完成![]() 步消元需做乘除法的总数为:
步消元需做乘除法的总数为:
![]()
次。回代过程共做乘除法的次数为:![]()
于是Gauss消去法中乘除法总次数为:![]()
当![]() 较大时,约为
较大时,约为![]() 次。例如当
次。例如当![]() 时,Gauss消去法中乘除运算约为2670次,可见Gauss消去法是计算机完全可以接受的方法。与Gauss消去法相反,克莱姆(Cramer)法则的运算量却大得使计算机无法承受。所以说Cramer法则对于求线性方程组的数值解是没有实际使用价值的。
时,Gauss消去法中乘除运算约为2670次,可见Gauss消去法是计算机完全可以接受的方法。与Gauss消去法相反,克莱姆(Cramer)法则的运算量却大得使计算机无法承受。所以说Cramer法则对于求线性方程组的数值解是没有实际使用价值的。
三 主元素的作用
称在Gauss消元过程中位于矩阵A(k)(k=l,2,…n)的主对角线(k,k)位置上的元素为主元素(简称主元)。由以上讨论得知,Gauss消元法的特点是每次都是按照系数矩阵的主元素的顺序依次将主对角线下方的元素消为零元素,若考虑高Gauss消元法的一种修正,即将主对角线下方和上方的元素都消为零元素,则这种方法称为高斯——若当(Gauss—Jordan)消元法(或无回代消元法)。在这种按顺序消元的过程中,可能会出现两个问题:
⑴ 一旦遇到某个主元为0,则消元过程便无法继续进行下去;
⑵ 即使主元素不为零,但与该元素所在列的对角线以下的各元素相比,它的绝对值很小(称为小主元),尽管消去运算可以进行下去,但在消元过程中要用其做除数,故其小小的舍入误差将会引起计算结果的严重扩散与失真。由第一章关于误差分析的知识,应当避免用较小的数做除数,以防止舍入误差的扩大,降低解的精度。
例如方程组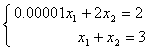 ,其准确至小数点后第9位的解为x1=2.000010000,x2=0.999898999。但若用Gauss消元法并在计算机编程计算过程中,用四位十进制浮点数求解(随着计算机的飞速发展,目前一般不使用定点表示而使用浮点表示法)用第1个方程消去第2个方程的x1,得:
,其准确至小数点后第9位的解为x1=2.000010000,x2=0.999898999。但若用Gauss消元法并在计算机编程计算过程中,用四位十进制浮点数求解(随着计算机的飞速发展,目前一般不使用定点表示而使用浮点表示法)用第1个方程消去第2个方程的x1,得:
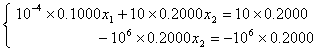
回代后解得x2=1,x1=0.0000,与精确解相比,结果严重失真,究其原因是用了“小”主元做除数,致使舍入误差增大,有效数字消失。因此,顺序Gauss消元法并非实用的消元方法。如果在消元前先交换两个方程的位置,变为:
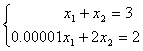
对此方程消元得三角方程组: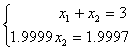
回代得解为x2=0.9999,x1=2.0001,结果与准确解非常接近。可见,第一种算法是不稳定的,第二种算法是稳定的。此例说明,在消元过程中,应避免选取绝对值较小的数做主元,否则可能导致结果错误、计算失败。
四 Gauss主元消元法
根据主元素的选取范围不同,通常又分为列主元Gauss消元法和全面主元Gauss消元法两种方法。为避免小主元作除数,在Gauss消元法中加入选列主元过程,即在第k步消元时,首先在A(k)的第k列主元以下(含主元)元素中挑选绝对值最大者,并通过行交换,使其位于主对角线上,并称之为第k步消元的列主元素,然后再进行消元计算。称每一步都按列选主元的Gauss消元法为Gauss列主元素消去法。在按列选主元的消元过程中,每次选主元时,仅依次按列选取绝对值最大的元素作为主元素,它只进行行交换,因而不产生未知数次序的调换。由于列主元素满足条件:![]() ,因此,列主元消去法能够避免Gauss消元过程中出现的两个问题,它是直接法中最常用的一种方法。误差分析与数值实验表明,用Gauss列主元素消去法解“良态”线性方程组,在绝大多数情况下,都可以得到令人满意的结果。
,因此,列主元消去法能够避免Gauss消元过程中出现的两个问题,它是直接法中最常用的一种方法。误差分析与数值实验表明,用Gauss列主元素消去法解“良态”线性方程组,在绝大多数情况下,都可以得到令人满意的结果。
此外,还有所谓全主元素高斯消去法,即在进行k步消元前,在A(k)的位于右下角的子矩阵中选取绝对值最大的元素作为主元素,再进行行和列的交换,把选到的主元素调至(k,k)位置,再按高斯消去过程进行消元。
由于全主元消去法每步所选主元的绝对值不小于列主元消去法同一步所选主元的绝对值,因而全主元消去法的求解结果更加可靠,但由于全主元素法在选主元时范围扩大,无疑需要花费大量的机器时间进行元素的比较,计算工作量比列主元素法大得多,而且在全主元素法中,又由于对增广矩阵进行了换列变换,未知量的排列顺序也要作相应的变换,这就使得算法的逻辑结构变得更复杂,需要占用的机时较多,因而程序较复杂。而列主元素高斯消去法的精度虽然稍低于全主元素法,但其计算简单,工作量小,又能满足精度要求,而且可以证明,列主元消去法的计算结果已比较理想,它与全主元素法同样具有良好的数值稳定性。因此到目前为止,在实际计算中,列主元素高斯消去法仍然是在计算机上解系数矩阵为中小型稠密矩阵的线性代数方程组的实用、有效、常用的方法之一。
五 消元过程中系数矩阵的分解
由线性代数知识,Gauss消元过程也可用矩阵乘法实现。分为两种情况讨论:
1 不带行交换的消元过程
令 ,
,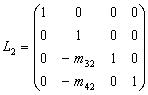 ,
,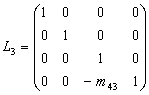
其中![]() 。则称
。则称![]() 是指标为k的初等下三角形矩阵(除第k列对角元以下元素外,其余的与单位矩阵E的元素相同),第k步消元(k=1,2,3,4),相当于用初等下三角形矩阵Lk左乘(A(k),b(k)),即:
是指标为k的初等下三角形矩阵(除第k列对角元以下元素外,其余的与单位矩阵E的元素相同),第k步消元(k=1,2,3,4),相当于用初等下三角形矩阵Lk左乘(A(k),b(k)),即:
Lk(A(k),b(k))=(A(k+1),b(k+1))
于是:LkA(k)=A(k+1),Lkb(k)=b(k+1) ,所以消元过程用矩阵运算表示为:
L
从而有:L
其中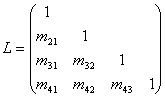 为单位下三角形矩阵,
为单位下三角形矩阵,
![]()
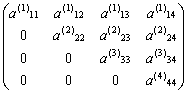 为上三角形矩阵,而且detA=detU。
为上三角形矩阵,而且detA=detU。
综上所述,不带行交换的Gauss消元过程产生了一个单位下三角形矩阵L和一个上三角形矩阵U,它们的乘积等于A。即:A=LU,称之为矩阵A的LU分解,又称为杜利特尔(Doolittle)分解。
我们把第k步消元时,在做行交换之前位于主对角线上的元素![]() 称为顺序主元。显然顺序主元
称为顺序主元。显然顺序主元![]() ≠0(
≠0(![]() 1,2,3,4),是不带行交换的消元过程完成的条件,因而也是系数矩阵A可以进行直接LU分解的条件。
1,2,3,4),是不带行交换的消元过程完成的条件,因而也是系数矩阵A可以进行直接LU分解的条件。
利用矩阵分块乘法得:![]()
其中![]() 、
、![]() 、
、![]() 依次是矩阵A、L的
依次是矩阵A、L的![]() 阶顺序主子阵,于是
阶顺序主子阵,于是![]() 阶顺序主子式:
阶顺序主子式:
![]()
用数学归纳法可推出:顺序主元![]() ≠0(
≠0(![]() 1,2,3,4)的充要条件是 A的各阶顺序主子式
1,2,3,4)的充要条件是 A的各阶顺序主子式![]() 皆不为0,且对于任意的
皆不为0,且对于任意的![]() 成立。于是有下面的定理:
成立。于是有下面的定理:
定理 设n阶方阵A的各阶顺序主子行列式均不为零,则A的LU分解式存在且唯一。
值得注意的是,在定理的条件下,消元过程完成后U可能是奇异矩阵,这时u44=![]() =0。所以u44是否为零对矩阵分解没有影响,但对回代求解能否进行起决定性作用。
=0。所以u44是否为零对矩阵分解没有影响,但对回代求解能否进行起决定性作用。
2 带有行交换的消元过程
设在第![]() 步消元时,先交换某两行后再消元,相当于先用一个交换两行的初等矩阵左乘增广矩阵,然后再消元,用矩阵运算表示为:
步消元时,先交换某两行后再消元,相当于先用一个交换两行的初等矩阵左乘增广矩阵,然后再消元,用矩阵运算表示为:
![]()
其中![]() 表示交换
表示交换![]() 两行的初等矩阵,
两行的初等矩阵,![]() 表示比
表示比![]() 小的某一行。
小的某一行。
于是带行交换的消元过程用矩阵运算表示为:![]() 。
。
最多交换3次。若交换3次,则![]() 一定等于4。将上式经过适当的恒等变形,可改写为:
一定等于4。将上式经过适当的恒等变形,可改写为:![]() 。利用矩阵乘法可以证明,
。利用矩阵乘法可以证明,![]() 也是一个单位下三角形矩阵,而P
也是一个单位下三角形矩阵,而P![]() ,称为排列阵。则有以下结论:
,称为排列阵。则有以下结论:
定理 设A为非奇异矩阵,则必存在排列矩阵P以及单位下三角形矩阵L和非奇异上三形矩阵U,使PA=LU。
即:带行交换的消元过程产生了矩阵PA的LU分解,相当于先对系数矩阵A施行消元过程中所需的行交换后再分解。只要A非奇异,带行交换的消元过程就可以进行到底。