定理（A＝LU的直接分解，无行交换变换）设无行交换变换的高斯消去法可求解一般线性方程组Ax＝b，则矩阵A可分解为一个下三角矩阵L和一个上三角矩阵U的乘积：A＝LU。而且L的对角线元素为1，U的对角线元素非零。得到L和U后，可通过如下步骤得到x：
1 利用前向替换法对方程组Ly＝b求解y
2 利用回代法对方程组Ux＝y求解x
证明：当执行高斯消去过程，并将B存入增广矩阵中（增广矩阵有N＋l列）时，上三角分解处理后的结果是等价的上三角线性方程组UX＝Y。矩阵L，U，B，Y有如下形式：
，
，
，
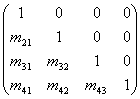注：如果只寻找L和U，可不需要增广矩阵的最后一列。
第1步：将系数存入增广矩阵。
的上标表示位于矩阵(r，c)处的值是第一次存放的：
第2步：消去第2行到第4行中的x1，并将用于消去行r中的x1的倍数mr1存入矩阵（r，l）处：for r＝2：4
mr1＝
/
；
＝mr1；
for c＝2：4＋1
＝－mr1×
；
end
end
新的元素写成
，表示在矩阵中的位置（r，c）处第2次存放的值。执行步骤2后的结果为：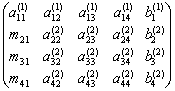
第3步：消去第3行到第4行中的x2，并将用于消去行r中x2的倍数mr2存入矩阵的（r，2）处：for r＝3：4
mr2＝
/
；
＝mr2；
for c＝3：4＋1
＝－mr2×
；end
end
新的元素写成，表示在矩阵中的位置（r，c）处第三次存放的值。执行步骤3后的结果为：
最后一步：消去第4行的x43，并将用于消去x3的倍数存入矩阵（4，3）处，
得到的最终结果是：
上三角处理过程执行完毕。要注意只使用了一个数组保存L和U中的元素。L中的对角线元素1没有保存，而且L中位于对角线上的元素0和U中位于对角线下的元素0也没有保存。只有用来重构L和U的系数元素才被保存。
对于一般线性方程组Ax＝b，一般步骤是第k＋1步：消去k＋1行到n行中的xk，并将用于消去k行中的xk的倍数存入矩阵（r，k）处：
for r＝k＋l：n
mrk＝；
ark＝mrk；
for c＝k＋1：n＋l
＝
－mrk×
；
end
end
将n行中的xk消去后得到的最终结果是：
矩阵A的LU分解的紧凑格式，还是以4阶矩阵来说明：
若A＝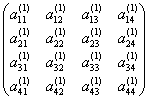
，
，
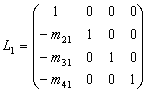
则L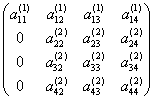
，
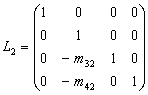
L
，
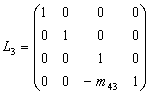
L＝U，则A＝L1－
令L= L1－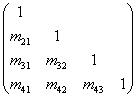
，则A＝LU。
其中Lk(k＝1，2，3)称为初等下三角矩阵，
。
以上过程可用下面的框图来表示：
|
⑴ ⑸ ⑹ ⑺ |
⑵ |
||
|
⑻ |
|||
|
⑾ ⑿ |
⒀ |
||
|
⒂ |
⒃ |
||
具体公式如下：第一步：行 
；列 
第二步：行 
；列 
第三步：行 
；
列 
第四步：行 
例：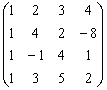
＝
解：第一步：行 ⑴ 
＝
＝1，⑵ 
＝
＝2，
⑶ 
＝
＝3，⑷ 
＝
＝4
列 ⑸ 
＝
＝
，⑹ 
＝
＝，⑺ 
＝
＝
第二步：行 ⑻ 
＝
＝
⑼ 
＝
＝
⑽ 
＝
＝
列 ⑾ 
＝
⑿ 
＝
第三步：行 ⒀ 
＝
＝
⒁ 
＝
＝
列 ⒂ 
＝
第四步：⒃ 
＝
＝
对于n阶矩阵A的LU分解元素，可由下面公式得出：
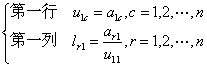
对于2到n行(或列)有：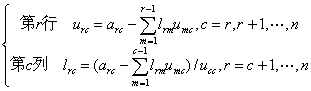
例 用Doolittle法解方程组：
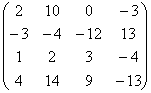
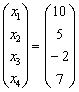
解(1)：A＝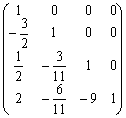
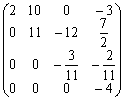
解Ly＝b得：y＝(
)T
解Ux＝y得：x＝(1，2，3，4)T
解(2)：用紧凑格式的Doolittle法求解，首先分解(A，b)
(A，b)＝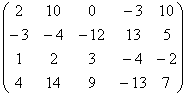
→
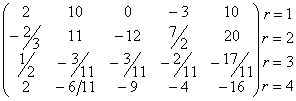
得y＝()T，再解Ux＝y，得x＝(1，2，3，4)T。
例 观察方程组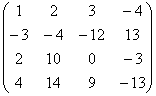
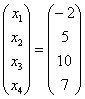与上例的区别。
解：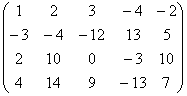
→
得y＝(
)T，再解Ux＝y，得x＝(1，2，3，4)T。
两个系数矩阵是经过交换1，3两行后得出的。产生的结果是LU分解式不同，y的解也不同，但x的解一定相同。
＝
×
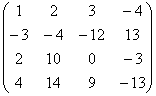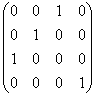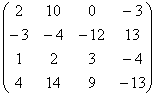
例 用部分选主元Doolittle法紧凑格式求解方程组AX＝B，其中：
，
，
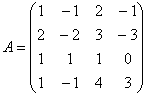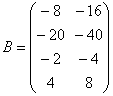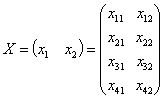
解：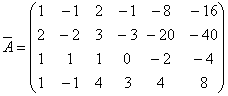 
，因为第一列的主元在第二行，因此，首先交换1，2两行：
再进行分解： 
如果直接计算第二步，则
，所以必须再次换行，然后继续分解。
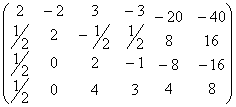
交换3，4两行后分解：
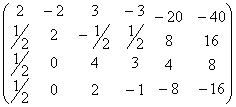
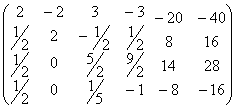
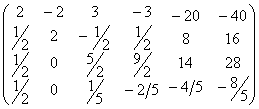
得Y＝(y1，y2)，其中y1＝(－20，8，14，－4/5)T，y2＝(－40，16，28，－8/5)T，最后再解UX＝Y，得
(－7，3，2，2)T，
(－14，6，4，4)T。
如果A是n阶对称矩阵，由定理2还可得如下分解定理：
定理 若A为n阶对称矩阵，且A的各阶顺序主子式都不为零，则A可惟一分解为：A＝LDLT，其中L为单位下三角阵，D为对角阵。
证明 因为A的各阶顺序主子式都不为零，所以A可惟一分解为：A＝LU
因为
，所以可将 U分解为：
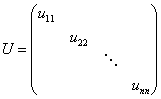
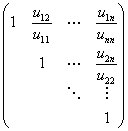
其中 D为对角矩阵，U1为单位上三角阵．于是：A＝LDU1＝L(DU1)
因为A为对称矩阵，所以，A＝AT＝U1TDTLT＝U1T(DLT)，由
A的 LU分解的惟一性即得：L＝U1T，即U1＝LT，故A＝LDLT。