在三次样条插值问题和常微分方程边值问题的数值解法中，都要借助于三对角方程组Ax＝g，其中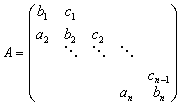
，
并且A满足条件：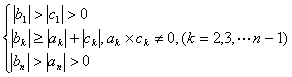
这时称A为对角占优的三对角矩阵。
以下我们还用四阶矩阵来说明具体的解法，则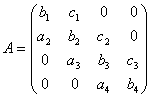
。
可以证明，三对角矩阵A可以分解为二对角的下三角矩阵L和二对角的上三角矩阵U的乘积。当U的对角元素为1时，属于Crout分解；当L的对角元素为1时，属于Doolittle分解。以下对A作Crout分解。
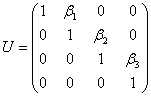
令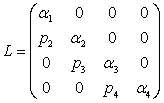
，
则有：＝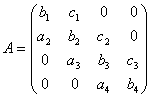
×
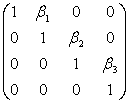
比较等式两边位置相同的元素，可得以下式子：
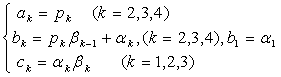
从上式解出：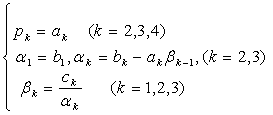
可见对A的分解只需要计算{
}和{
}就可以了，而且需按
→
→
→
→
→
→
的递推过程进行。
解方程组Ax＝g可化为解如下两个三角形方程组：
1 解方程组Ly＝g，即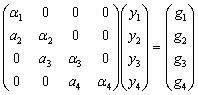
，列出方程组并解之。
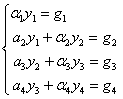，解得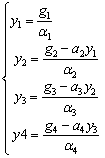
把下标从小到大求yr的过程，形象地称之为“追”的过程
2 解方程组Ux＝y，即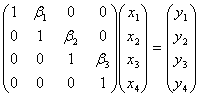
，列出方程组并解之。
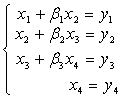，解得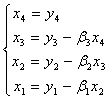
把下标从大到小求解
的回代过程为“赶”的过程。因此，称由以上过程求解三对角方程组Ax＝g的方法为追赶法。
例 用追赶法解线性方程组
解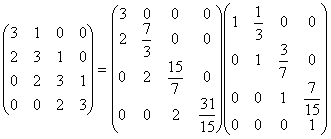 
，
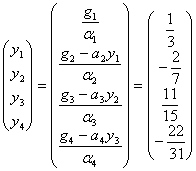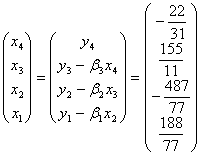
具体计算如下：
，
，
，
，
，
，
，
，
，
，
，
，
，
附MATLAB程序
% 用追赶法解4阶三对角方程
a=[0 2 2 2];b=[3 3 3 3];c=[1
1 1 0];g=[1 0 1 0];
d=b(1);g(1)=g(1)/d;
for k=2:4,
c(k-1)=c(k-1)/d;d=b(k)-a(k)*c(k-1);
g(k)=(g(k)-a(k)*g(k-1))/d;
end
clear d a b
for k=3:-1:1,
g(k)=g(k)-c(k)*g(k+1);
end
g
g=0.5806 -0.7419 1.0645 -0.7097
>> A=[3 1 0 0;2 3 1 0;0
2 3 1;0 0 2 3];
b=[1 0 1 0]';A\b
ans =0.5806 -0.7419 1.0645 -0.7097
>> A=[4 1 0 0 0;1 4 1 0
0;0 1 4 1 0;0 0 1 4 1;0 0 0 1 4];
b=[2 1 1 1 2]';A\b
ans =0.4808
0.0769
0.2115
0.0769
0.4808
例 A=[2 -1 0 0;-1 2 -1 0;0 -1 2 -1;0 0 -1
2];
b=[1 0 1 0]';A\b
ans =1.2000
1.4000
1.6000
0.8000
对于n阶矩阵A有以下公式：
从上式解出：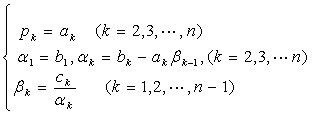
可见对A的分解只需要计算{}和{}就可以了，而且需按→→→→…→
→
→
的递推过程进行。
例 用追赶法解线性方程组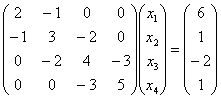
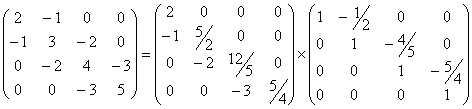
追的过程y＝(3，8/5，1/2，2)T，赶的过程x＝(5，4，3，2)T
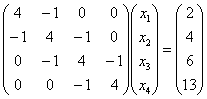，x=(1,2,3,4)T