在计算方程组Ax＝b的数值解时，系数矩阵A和右端向量b作为初始数据将对计算结果产生直接影响。由于计算机机器数的位数有限，初始数据转换为机器数的误差以及运算过程中的舍人误差都会对计算结果的精确性产生影响。所以，用直接法求出的数值解，大多数情况下是方程组的近似解而不是准确解。在初始数据精度不变，机器数位数相同时，计算结果的精确程度和所用算法（数值稳定的算法或不稳定的算法）有密切的关系。另一方面，在所用算法相同，初始数据精度相同，机器数位数相同的条件下，不同的问题所得的计算结果的精度也会有很大的差别。这种情况表现出方程组本身的一种固有特性。例如，一个方程组右端向量中数据的微小变化（数学上称为摄动），可能引起方程组准确解的微小变化，但有时也可能会引起很大变化。
例如，对于线性方程组：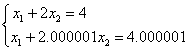
显然，
＝2，
＝1是方程组惟一的精确解。如果由于某种原因致使第2个方
程右端产生一个小的变化：从4.000 001变为4.000 01(由原来的小数点后六位数变为五位数)，于是方程组：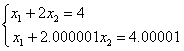
惟一的精确解变为＝－16，＝10，两个解之间的差距是不可忽视的。
求这一类方程组的数值解问题就是一个病态问题。这是因为方程组系数矩阵的性态所引起的，所以也称这样的方程组的系数矩阵为病态矩阵。对于病态问题，人们往往需要对问题作一些预处理，或选择高精度的算法，或用双精度机器数进行计算，以减小由于病态对计算结果的影响。
所谓病态问题是指，如果计算问题本身对于初始数据的微小变化，就能引起计算结果的剧烈变化，则称该问题为病态问题。反之，称为良态问题。