§2

§2.2 迭代法

前面介绍的直接法是在不考虑舍入误差时，求方程组精确解的方法，由于这种方法在求解的过程中，系数矩阵A在不断地变动，如果A的阶数较大时，占用计算机的内存就很大，而且程序比较复杂，对程序设计的技巧要求也较高，因此，我们希望找一种在求解过程中，原始系数矩阵A在计算过程中始终不变，且程序设计又不复杂的求解方法，这种方法就是迭代法。迭代是计算机科学中的一个基本要素，它是指不断重复执行一个计算过程，直到找到答案。具体地说，迭代法就是用某种极限过程去逐步逼近线性方程组精确解的方法，即是从一个初始向量出发，按照一定的迭代格式产生一个向量序列｛｝，使其收敛到方程组Ax＝b解。在求解线性、非线性及微分方程过程中，都会用到迭代技术。

迭代解法的优点是所需计算机存储单元少，编制程序简单，非常适用于求解大型稀疏系数矩阵的方程组（尤其是微分方程离散后得到的大型方程组），是计算机常用的算法之一，但迭代法存在收敛性及收敛速度问题。本节先介绍迭代法的基本思想，再介绍几种在解线性方程组时常用的迭代法，主要有Jacobi迭代法、Gauss-Seidel迭代法、SOR（超松驰）迭代法等，接下来简单讨论迭代法的收敛性和误差估计，最后介绍判断迭代收敛的几个常用条件。

2.2.1 迭代法的基本思想

设有n阶线性方程组：Ax＝b的系数矩阵A为非奇异矩阵，写出它的一个等价形式：x＝Mx＋g 　　（式2.2.1）

任意给出x的一个值称为初始向量，代入（式2.2.1）的右边，算出的结果记为，再将代入（式2.2.1）的右边，算得的结果记为，一般地有：

＝M＋g （式2.2.2）

上式称为Ax＝b的迭代格式，M称为迭代矩阵。由出发得到的迭代序列，，…如果有极限，即存在x使：，则称迭代格式（式2.2.2）收敛，此时x就是Ax＝b的解。其中极限的意思是指或∣－X_i∣→0，i=1，2，…，n。由于对方程组Ax＝b可以构造出收敛的迭代格式或不收敛的迭代格式，并且迭代总是只能进行有限步，因此，用迭代法求解线性方程组时面临两个问题：

（1）如何构造一个收敛的迭代格式；

（2）何时终止迭代得到满意的近似解。

下面先介绍几种常用的迭代格式。

2.2.2 雅各比（Jacobi）迭代法

雅各比迭代法又称为简单迭代法。具体方法可通过以下例题给出。

【例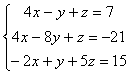2.2.1】求解方程组　　　　　　　

若将方程组表示成如下形式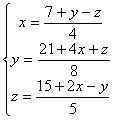

就给出了雅各比迭代过程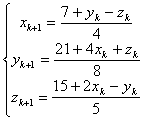 (式2.2.3)

如果从初始点开始，即将代入(式2.2.3)每个方程的右边，可得如下新值：，

，。新的点比更接近极限值。使用(式2.2.3)不断的迭代，则产生的点序列将收敛到解。

这个过程就称为雅各比迭代法，可以用来求解某些类型的线性方程组。下面讨论一般情况。

设有方程组Ax＝b，其中

A＝，x＝，b＝

A为非奇异矩阵。当A为三阶方阵时，可简化为：

A＝，x＝，b＝

假设≠0，r＝1，2，3，令：＝－／，r≠j，＝／，

即：，，，

，，，

则方程组Ax＝b可以写成迭代格式：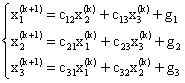

这就是雅各比迭代格式。若记：

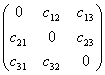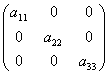C＝，D＝，g＝

因为A＝D(E－C)，所以C＝(D－A)＝E－A，而g＝b，因此有：

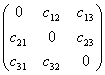C＝＝(D－A)

＝（－）

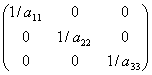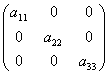雅各比迭代格式可以用矩阵表示为：x^(k+1)＝Cx^(k)＋g，其中迭代矩阵M＝C。

如果选取初始向量x⁽⁰⁾＝（x₁⁽⁰⁾，x₂⁽⁰⁾，x₃⁽⁰⁾），则可得到迭代序列｛x^(k)｝，若该迭代序列收敛到x，则有：x＝Cx＋g，即x－Cx＝g，从而(E－C)x＝g，两边同乘矩阵D后，D(E－C)＝Dg，即Ax＝b。这表明，收敛的迭代序列的极限x就是方程组Ax＝b的解。

有的时候雅各比迭代法也会无效。重新排列【例2.2.1】，可得如下方程组，仍然利用雅各比迭代法，还以为初始点，则产生一个发散的点序列。

【例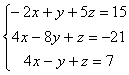2.2.2】求解方程组

解：雅各比迭代公式为：

经计算，，，以后结果见下表

k	x_k	y_k	z_k
0	1.0	2.0	2.0
1	-1.5	3.375	5.0
2	6.687	2.5	16.375
3	34.6875	8.015625	-17.25
4	-46.617188	17.8125	-123.73438
5	-307.929688	-36.150391	211.28125
6	502.62793	-124.929688	1202.56836

计算结果更加远离解(2，4，3)。

如果设n阶线性方程组为：Ax＝b，则Jacobi迭代法的迭代公式如下：

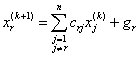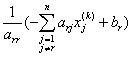＝， (式2.2.4)

与之对应的Jacobi迭代公式的矩阵表示形式为：x^(k+1)＝Mx^(k)＋g

其中，M称为Jacobi迭代矩阵，M＝－(L＋U)，g=b，D为对角矩阵，L与U分别为严格下三角、严格上三角矩阵。据此，就可以编写实现Jacobi迭代法的M函数，如下所示：

ykbdd.m

function s=ykbdd(a,b,x0,eps)

% jacobi迭代法解线性方程组

%a为系数矩阵，b为方程组ax＝b中的右边的矩阵b，xo为迭代初值

If nargin＝＝3

eps=1.0e-6;

elseif nargin<3

error

return

end

D=diag(diag(a)); %求出对角矩阵

D=inv(D); %求出对角矩阵的逆

L=tril(a,-1); %求出严格下三角矩阵

U=triu(a,1); %求出严格上三角矩阵

B=-D*(L+U);

f=D*b;

S=B*x0+f;

While norm（s－x0）＞＝eps

x0=S;

s=B*x0+f;

end

return

【例2.2.3】用上面编写的jacobi函数求解下列方程组

10xl－2x2－x3=3

－2x1＋10x2－x3＝15

－x1－2x2＋5x3=10

用MATLAB来实现，如下所示：

A=[10 -2 -1;-2 10 -1;-1 -2 5];

b=[3 15 10]';

x0=[0 0 0]';

eps=0.0001;

s=ykbdd(A,b,x0,eps)

1．0000 2．0000 3．0000

【例2.2.4】A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-1 3 2 7];

b=[-2 -6 6 12]';

x=[0 0 0 0]';y=x;

for k=1:21

for m=1:4

s=x(m);x(m)=0;

y(m)=(b(m)-A(m,:)*x)/A(m,m);x(m)=s;

end

eorr=norm(y-x,inf);x=y,

end

具体计算数据如下：

x1 = -0.4000 -0.7500 -1.5000 1.7143

x2 = 0.1357 -1.1054 -1.6536 2.4071

x3 = 0.4532 -1.4799 -1.5152 2.6798

x 4= 0.6649 -1.6788 -1.3167 2.8462

x 5= 0.8109 -1.8190 -1.2059 2.9050

x 6= 0.8846 -1.8914 -1.1140 2.9542

x 7= 0.9372 -1.9397 -1.0717 2.9695

x 8= 0.9614 -1.9639 -1.0382 2.9857

x 9= 0.9794 -1.9802 -1.0241 2.9899

x 10= 0.9872 -1.9881 -1.0125 2.9955

x 11= 0.9933 -1.9935 -1.0080 2.9966

x 12= 0.9958 -1.9961 -1.0041 2.9986

x 13= 0.9978 -1.9979 -1.0027 2.9989

x 14= 0.9986 -1.9987 -1.0013 2.9995

x15 = 0.9993 -1.9993 -1.0009 2.9996

x16 = 0.9995 -1.9996 -1.0004 2.9999

x17 = 0.9998 -1.9998 -1.0003 2.9999

x18 = 0.9998 -1.9999 -1.0001 3.0000

x19 = 0.9999 -1.9999 -1.0001 3.0000

x20 = 0.9999 -2.0000 -1.0000 3.0000

x21 = 1.0000 -2.0000 -1.0000 3.0000

2.2.3 高斯—赛德尔（Gauss—Seidel）迭代法

有时可以通过其他方法使收敛速度加快，对雅各比迭代公式稍加改进，就可得到实用上更为有效的计算公式。

观察【例2.2.1】中雅各比迭代的计算过程可以看出，由迭代产生的三个序列，，分别收敛到2，4，3。因此可以认为是比更接近精确解的近似值，所以在计算时，用来代换是合理的。同理可用和用于计算。这样既可以节省内存，又给编制程序带来更多方便。不仅如此，由于迭代序列收敛，一般地，x^(k+1)比x^(k)更接近精确解，因此，这种方法可以加快收敛速度。这种方法就是所谓高斯—赛德尔法代法，又简称为赛德尔迭代法。其迭代格式为：

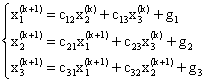　（式2.2.5）

（设A为三阶方阵）。公式中的与雅各比迭代公式中的意义相同。

若记C＝L＋U，其中L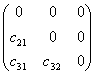＝，U＝

则赛德尔迭代过程可用矩阵表示为：

＝L＋U＋g k＝1,2,3 （式2.2.6）

由于E－L可逆，右边第一项移项后，同乘E－L的逆矩阵可得：

＝U⁾＋g ＝1,2,3

矩阵M＝U称为赛德尔迭代法的迭代矩阵。应当注意的是，当交换方程和未知量的顺序时，都会影响到赛德尔迭代法的计算结果。

% 高斯——赛德尔迭代法　例

A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-1 3 2 7];b=[-2 -6 6 12]';x=[0 0 0 0]';y=x;

for k=1:10

eorr=0;

for m=1:4

s=x(m);x(m)=0;

x(m)=(b(m)-A(m,:)*x)/A(m,m);

erro=max(abs(s-x(m)),eorr);

end

x',pause,eorr

end

ans = -0.4000 -0.6500 -1.2750 2.3000

0.3950 -1.5519 -1.2003 2.7788

0.7818 -1.8374 -1.0805 2.9222

0.9203 -1.9408 -1.0301 2.9718

0.9709 -1.9784 -1.0110 2.9897

0.9894 -1.9921 -1.0040 2.9963

0.9961 -1.9971 -1.0015 2.9986

0.9986 -1.9989 -1.0005 2.9995

0.9995 -1.9996 -1.0002 2.9998

0.9998 -1.9999 -1.0001 2.9999

0.9999 -1.9999 -1.0000 3.0000

1.0000 -2.0000 -1.0000 3.0000

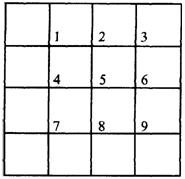使用下面的熟知的例子说明解线性方程组的Gauss-Seidel迭代。一条狗遗失在一个方形的多通道迷宫中，在每一个交叉点处它随机地选择一个方向并前进至下一个交叉点，在那儿它又随机地选一个方向等等。一条狗从交叉点处出发最终出现在南面边界上的概率是多少？

假定恰好有 9个内部交叉点，如图所示。

令P₁代表狗从第一个交叉点出发最终出现在南

边上的概率，令P₂…，P₉类似地被定义。假设

在到达的每个交叉点，狗等可能地随意选一个

方向，并假设只要它到达了任何一个出口它的

游动就算结束。概率论于是为P_k提出下面的9

个方程：，

，，

，

保留方程的这种形式，我们选择P_k的初始逼近值。这里有可能作出明智的猜想，但是仍假定对所有的k我们取的是平凡的初始值P_k＝0。按列出的顺序取方程，我们逐个地计算第二次的逼近值。首先P₁算出来为零。接着P₂，…，P₆也如此。但是这之后我们得到：，，，这样每个P_k的第二次逼近值就有了。注意在计算P₈和P₉时分别用到P₇和P₈的最新逼近值。看来使用早些时的逼近值意义不大。这个（使用最新值的）过程更快地导出正确结果。现在以同样的方式逐次得到逼近值，迭代持续到在所要求的小数位不出现进一步的变化为止。工作到3位，得到下表中的结果。注意算出的P₅为0.250，这意味着从中心出发的狗之中有1/4会出现在南面的边界上。从对称性的角度，这是合理的。可以将所有的9个值四代入原始方程作进一步检验，来看诸残量是否是小量。用MATLAB解得如下：

0.0714 0.0982 0.0714 0.1875 0.2500 0.1875 0.4286 0.5268 0.4286

用Gauss-Seidel方法迭代，可得以下计算数据：

k	P1	P2	P3	P4	P5	P6	P7	P8	P9
0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0.25	0.312	0.328
2	0	0	0	0.062	0.078	0.082	0.328	0.394	0.328
3	0.016	0.024	0.027	0.106	0.152	0.127	0.375	0.464	0.398
4	0.032	0.053	0.045	0.140	0.196	0.160	0.401	0.499	0.415
5	0.048	0.072	0.058	0.161	0.223	0.174	0.415	0.513	0.422
6	0.058	0.085	0.065	0.174	0.236	0.181	0.422	0.520	0.425
7	0.065	0.092	0.068	0.181	0.244	0.184	0.425	0.524	0.427
8	0.068	0.095	0.070	0.184	0.247	0.186	0.427	0.525	0.428
9	0.070	0.097	0.071	0.186	0.245	0.187	0.428	0.526	0.428
10	0.071	0.098	0.071	0.187	0.250	0.187	0.428	0.526	0.428

在Gauss-Seidel方法的这一例子里9个方程中的每一个都以下面的形式出现： Pi＝…，并且以此形式来校正对只的逼近，用到的是其他分量的最新值。值得注意的是在每个方程里左边的那个未知量有最大的系数。

§2.2 迭 代 法

§2.2 迭代法