§2.３　范数与条件数

在分析方程组的解的误差及迭代法的收敛时，常产生一个问题，即如何判断向量x的“大小”，对矩阵也有类似的问题。本节介绍n维向量和n阶矩阵的范数。

2.３.1　向量范数

定义2.3.1　设x和y是n维向量空间Rⁿ中的任意向量，向量范数是定义在Rⁿ上的一个实值函数，它满足以下三个条件：

(1)　非负性　≥０，当且仅当x＝0时，等号成立。

(2) 齐次性　对于任意实数k，＝。

(3) 三角不等式　。

容易看出，向量范数是以n维向量空间Rⁿ为定义域的一种特殊函数——非负实函数，实数的绝对值，复数的模，三维向量的模都满足以上三条，n维向量的范数概念是它们的自然推广。

设x＝(x₁，x₂，…，x_n)^T，在n维向量空间Rⁿ中常使用的向量范数有三种：

(1) １范数：＝

(2) 欧几里德范数（或2范数）：＝

(3) 无穷范数（或最大模范数）：＝

其中2范数就是按向量内积定义的范数，一般我们把定义了范数的向量空间，称为赋范向量空间。可以证明，以上三种范数都满足定义2.3.1。由定义可知，同一个向量在不同意义下的范数值可以是不同的。

　　【例2.3.1】x＝(1，－2，1)^T，则＝４，＝６，＝２

y＝(1，0，0)^T, 则＝＝＝1

定义2.3.2　设有向量序列x⁽¹⁾，x⁽²⁾，…，x^(k)，…，如果存在同维向量x，使得：，其中表示向量的任意一种范数，则称向量序列依范数收敛于向量x，记为：。

容易证明，对于前面三种范数中的任意一种，等价于，r =1，2，…，n。也就是说，向量序列的依范数收敛等价于依分量收敛。

由例2.3.1可知，一个向量在不同意义下的范数值可以是不同的，但它们在向量序列的收敛性上是等价的，即向量序列按某一种范数收敛时，按另外的两种范数也一定收敛。

关于向量范数我们有以下一些结论。

定理2.3.1 对于任何x∈Rⁿ，有≥≥≥

定义2.3.3 对于任意两种范数和，若存在正常数c₁与c₂使得：

≤c₁且 ≤c₂或≤≤c₁

则称两个范数是等价的，范数的等价关系具有传递性。

定理2.3.2 n维向量空间Rⁿ上的一切向量范数相互等价。

从以上定理看出，当向量的任一种范数趋于零时，其它各种范数也趋于零。因此讨论向量序列的收敛性时，可不指明使用的何种范数；证明时，也只要就某一种等价范数证明就行了

2.３.2　矩阵范数

利用向量范数，可以定义n阶方阵A的矩阵范数。

定义2.3.４ 设A是n阶方阵，x∈Rⁿ，令＝

为矩阵A的范数。

它可以理解为A作为线性变换，作用于不同的x后，能将x的范数放大的最大倍数。这样定义的范数有如下性质：

　　(1)　 ≥0 并且，当且仅当 A是零矩阵时，等号成立；

　 (2)　 ，其中k是任意一个实数；

　　(3)　设A，B是两个同阶方阵，有：；

(4) 设A，B是两个同阶方阵，有：；

(5) 设A是n阶方阵，x∈Rⁿ，有：

矩阵范数最常用的有以下几种：

(1)　列和(1)范数：

(2)　行和(无穷)范数：

(3)　谱(2)范数：，其中是 A^TA的绝对值最大特征值；

(4)　F范数：

它们分别与向量的范数对应，即用一种向量范数可定义相应的矩阵范数。

矩阵范数还有一种与向量范数类似的定义方式，即将满足前4条性质的实数称为矩阵范数。可以证明上述范数必定满足这4个条件。这样，将第5条性质称为相容性，即满足条件5的向量范数与矩阵范数是相容的。对于上面定义的向量范数与矩阵范数是相容的，但对于任意定义的范数，相容性未必成立。

【例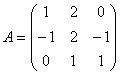2.3.2】设矩阵，求。

解：列范数　＝max{2,5,2}＝5，行范数　＝max{3,4,2}＝4

谱范数　＝

类似向量序列的收敛，可以定义矩阵序列的收敛。

定义2.3.5 设有矩阵序列A⁽¹⁾，A⁽²⁾，…，A^(k)，…，如果存在同阶矩阵A，满足：＝0，则称矩阵序列收敛于n阶矩阵A。

定理2.3.3 设A^(k)＝()_n×n，A＝()_n×n，则矩阵序列A^(k)收敛于矩阵A的充要条件是：，r，c=1，2，…，n。

2.３.3　谱半径

定义2.3.6 设A为n阶方阵，A的特征值为(＝l，2，…，n)，则称：

为A的谱半径。

定理2.3.4 矩阵谱半径和矩阵范数有如下关系：。

证 设是A的任一特征值，为对应的特征向量，则有：，

两边取任意范数，并利用矩阵范数的相容性，可得：

因为0，所以＞0，上式两边消去后有：，＝l，2，…，n，所以：。

定理2.3.5 设A为n阶方阵，A的各次幂组成的矩阵序列E，A，A²，…，A^r，…收敛于零，即＝0的充要条件是＜l。

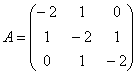【例2.3.3】设，求，，，。

解 显然，列范数＝4，行范数＝4，下面计算2范数(谱范数)。

由于矩阵A为对称矩阵，即A^T＝A，所以有；

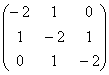
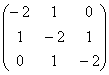
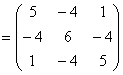
令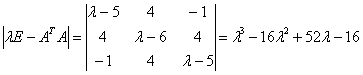

＝0

可得，，，显然之模最大。

所以2范数。

下面计算A的谱半径，

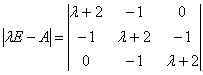
所以，，，显然之模最大，

所以＝。

这里，我们指出，对于实对称矩阵A，有＝。

2.３.4　条件数及病态方程组

线性方程组Ax＝b的解是由系数阵A及右端常数向量b决定的。由实际问题中得到的方程组中A的元素和b的分量，总不可避免地带有误差，因此也必然对解向量x产生影响。这就提出一个问题：当A有误差A，b有误差b时，解向量x有多大误差？即当A和b有微小变化时，x的变化有多大？若A和b的微小变化，也只导致x的微小变化，则称此问题是“良态”的；反之，若A和b的微小变化会导致x的很大变化，则称此问题为“病态”问题。在以下的讨论中，设A非奇异，b≠0，所以‖x‖≠0。

⑴ 设Ax＝b中仅b向量有误差b，对应的解x发生误差x即：

A(x＋x)＝b＋b

注意到Ax＝b，所以有：Ax＝b。若A非奇异，有x＝b，则可得：

，又因为＝，所以，

上面两式相除，有：， (*)

即x的相对误差小于等于b的相对误差的倍。

⑵ A有误差A，b无误差，此时解为：

同理注意到Ax＝b，有：Ax＋Ax＋Ax＝0，两边同乘，并移项得：

x＝－Ax－Ax

两边除以，得：

一般讲A是一个微小元素组成的矩阵，故相当小，1－＞0总能成立，解出下式： (**)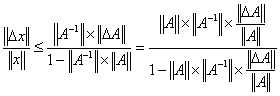

它反映了x的相对误差和A的相对误差的关系，不难分析出，当‖A‖增大时，右端分子增大，分母减小，右端的值增大。

⑶ 由以上分析不难看出，当b和A一定时，的大小，决定了x的相对误差限。越大时，x可能产生的相对误差越大，即问题的“病态”程度越严重。同时，我们看出，Ax＝b的“病态”程度，与A的元素有关，而与b的分量是无关的。为此，我们有以下定义：

定义2.3.6 设A为n阶非奇异方阵，则称为A的条件数，记为：

cond(A)＝

由此，式(*)，(**)可分别改写为：

，

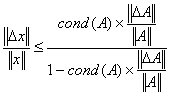
由于选用的范数不同，条件数也不同，所以在有必要时，可记为：

，(，，)

由于1＝，可知cond(A)总是大于等于1的数。条件数反映了方程组的“病态”程度。条件数越小，方程组的性态越好；条件数很大时，称方程组为病态方程组。但多大的条件数才算病态则应视具体问题而定，病态的说法只是相对而言。

条件数的计算是困难的，这首先在于要算A的逆，而求A的逆比解Ax＝b的工作量还大，当A确实为病态时，A的逆也求不准确；其次要求范数，特别是求2范数又十分困难，因此实际工作中一般不先去判断方程组的病态。但是必须明白，在解决实际问题的全过程中，发现结果有问题，同时数学模型中有线性方程组出现，则方程组的病态可能是出问题的环节之一。病态方程组无论选用什么方法去解，都不能根本解决原始误差的扩大，即使采用全主元消元法也不行。可以试用加大计算机字长，比如用双精度字长计算，或可使问题相对得到解决。如仍不行，则最好考虑修改数学模型，避开病态方程组。如在拟合问题中出现的正规方程组，就往往呈现病态，此时解决问题的方法之一是避开正规方程组，采用正交多项式拟合的方法，尽管后者比前者在理论上和实际计算中都复杂得多。

【例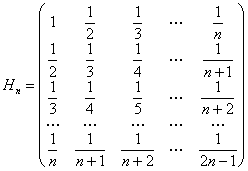2.3.4】n阶希尔伯特矩阵

当n较高时，是有名的病态矩阵。在函数逼近时，有时得到方程组H_nx＝b，当n稍高，用任何方法都难以解出理想的结果。考查它的条件数如下表：

希尔伯特矩阵条件数表

N	cond1(Hn)	cond2(Hn)	cond∞(Hn)	cond2(Hn)
3	748	5.24×10^2	748
4		1.55×10^4
5		4.77×10^5
6		1.50×10^7	2.9×10^7
7		4.75×10^8
8		1.53×10^10
9		4.93×10^11
10		1.60×10^13

可见H_n在n稍高时，即呈严重病态。

【例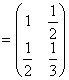2.3.5】求H₂的条件数(H₂)，(H₂)，(H₂)。

解：⑴令，解得：

，因为H₂对称，则1.2676

由于，则令：

，解得：

同理对称，所以15.2111

则H₂的条件数cond₂(H₂)＝×≈1.2676×15.2111≈1902816

⑵ ，18，所以cond₁(H₂)＝×＝27

⑶ 同理(H₂)＝×＝27。

【例2.3.6】求H₃的条件数(H₃)，(H₃)，(H₃)。

解 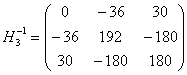，，，由此可得：(H₃)＝11/6×408＝748。同理，(H₃)＝748。