§3.1  方程求根与二分法

 

为了确定根的初值，首先必须确定根的分布范围，即确定根的范围或对根的分布进行隔离。在上述基础上，采取适当的数值方法确定出具有一定精度要求的初值。对于代数方程，其根的个数（实的或复的）与其次数相同，并且已有许多关于确定根的范围及确定所在范围内根的个数的定理和有效方法，都可取用。至于超越方程，其根可能是一个、几个或无解，且没有什么固定的确根方法。

求方程根的问题，就几何上讲，就是求曲线与轴交点的横坐标，作为一个根位于某个子区间内的标志常依据下面的定理。

定理3.1.1 设为区间上的单值连续函数，若，

则在区间内至少有一个实根。如果是单调函数，则仅有一个实根。

运用上面定理，就可确定根所在的子区间，有以下几种方法。

 

3.1.1图解法

此法通过画出的略图，从而确定出曲线与轴交点的大致位置。为使画图简便，可将0，分解成的形式，其中与是比较容易画出其图形的函数。这时与两曲线交点的横坐标所在的子区间即为含根区间。

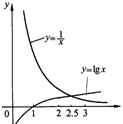
例如：xlnx－1＝0，就可以改写为lnx＝1/x，再分别画出对数曲线lnx与双曲线1/x，则如图所示它们交点的横坐标位区间[1，2]内。

 

3.1.2 扫描法

对于给定的 及含根区间，从A出发，以步长h＝(n为正整数)，在区间内取定节点：xk＝x0＋kh，(k＝0，1，2，…，n)，然后从左至右检查的符号，如发现与异号，则得到一个有根子区间，同法继续下去，就可在区间内找出包含根的全部子区间。

用这种逐步搜索法进行实根隔离的关键是选取合适的步长h，如果h过大，则可能遗漏根；如果h太小，虽可得到较小的有根子区间，但工作量较大。

 

3.1.3     波尔察诺(Bolzano)二分法

3.1.4      

为了获得指定精度要求的初值，可在以上隔离根的基础上采用二分法进一步缩小含根子区间，方法如下。

设为含根子区间，对于根的误差要求为，令，，计算，。起始区间必须满足与符号相反的条件。由于连续函数的图形无间断，所以它会在零点x＝r处跨过x轴，且r在区间内。通过二分法可将区间内的端点逐步逼近零点，直到得到一个任意小的包含零点的间隔。二分法判定过程的第一步是选择中点c＝(a＋b)/2，然后分析可能存在的三种情况：① 如果和符号相同，则在区间内存在零点；

② 如果和符号相同，则在区间内存在零点；

③ 如果0，则是零点。

如果情况①或情况②发生，则表示找到一个比原先区间范围小一半的区间，它包含根，并称为对区间进行压缩，为了持续此过程，需要对新的更小区间进行重新标号，重复执行直到区间足够小。由于二分法过程包括嵌套区间间隔和它们的中点，所以采用如下符号来表示过程的细节：

是起始区间，它包含零点，同时是中点；

是第一个区间，它包含零点，同时是中点，区间的宽度范围是的一半；

是第二个区间，它包含零点，同时是中点，区间的宽度

范围是的一半；

是第n个区间 (包含r，并有中点)后，它也包括r，宽度范围是的一半。

经n次对分后获得如下含根区间：，，，…，，其区间长度逐次减半，设经n次对分后，其区间长度已小于，则有以下估计n的公式：，或，这时我们可在区间内任意取定一点x作为函数的根。

编制程序可按以下过程进行：

    ①取的中点，计算。

    ②若＞0，则取；否则取。

    ③若b－a＞转向①；否则结束。

任取，如可令，则就是近似解。

【例3.1.1】在无阻尼强迫振荡的研究中会碰到函数h(x)＝xsinx，寻找在区间[0，2]内的值x，满足h(x)＝1，函数sinx用弧度计算。

解 利用二分法寻找函数f(x)＝xsinx－l的零点。初始值a0＝0，b0＝2。计算：

f(0)＝－1.000000和f(2)＝0.818595，

因此，f(x)＝0的一个根位于区间[0，2]内。在中点c0＝1处，f(c0)＝－0.158529，所以从左边压缩，令a1＝c0＝1，b1＝b0＝2。因此区间改变为[a1，b1]＝[1，2]。接下来，计算在中点c1＝1.5处，f(c1)＝0.496242，所以从右边压缩，使得a2＝a1＝1， b2＝c1＝1.5。以此类推，按这样的方法，可得到序列ck，它收敛到r＝l.114157141。下表给出了用二分法求解xsinx－1＝0的计算样本。

k

左端点，ak

中点，ck

右端点，bk

函数值，f(ck)

0

0

1

2

－0.158529

1

1.0

1.5

2.0

0.496242

2

1.00

1.25

1.50

0.186231

3

1.000

1.125

1.250

0.015051

4

1.0000

1.0625

1.1250

－0.071827

5

1.06250

1.09375

1.12500

－0.028362

6

1.093750

1.109375

1.125000

－0.006643

7

1.1093750

1.1171875

1.1250000

0.004208

8

1.10937500

1.11328125

1.11718750

－0.001216

9

1.11328125

1.115234375

1.117187500

0.001496

…

…

…

…

…

【例3.1.2】考虑一个与复利相关的题目。假设每个月存钱P元，年利率为I。存了N次之后，钱的总数为：

＋…＋

解 方程右边的第一项是最初存的钱数P；

第二项为：得到一次利息的第一次报酬 (其中是将年利换算成月利)，再加上本次所存的钱数P，共计，前两项总和为：；

第三项为：得到两次利息的第二次报酬，加上本次所存的钱数P，共计：

则前三项总和为：＋；

以此类推，最后一项是：得到N－1次利息的最后一次报酬，加上本次所存的钱数P，共计：。

求解N项几何级数和的公式是：

则可将A写成如下形式：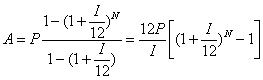

下面的例子使用应付年金的公式而且需要一系列的重复计算来得到答案。

【例3.1.3】每个月存款200元，按复利计息，持续存m年，希望在35年后报酬和利息的总值达到25万元左右。问年利率I为多少时可满足需求？

设N＝420，则A是I的函数。初始假设I＝0.035和I＝0.045，执行一系列的计算来接近最终答案。从I＝0.04开始可得：

[12*200/0.035][(1 + 0.035/12)^(12*35)]= 233013

由于此结果比目标小，接下来试验I＝0.045，计算如下：

[12*200/0.045][(1 + 0.045/12)^420]=256882.

结果又有些高，因此取中间值I1＝(0.035+0.045)/2＝0.04，计算如下：

[12*200/0.04][(1 + 0.04/12)^420]=242746

这个结果比目标小，这样可得出期望的利率在区间[0.04，0.05]内。再取中间值    I2＝(0.04+0.045)/2＝0.0425，计算如下：

[12*200/0.0425][(1 + 0.0425/12)^420]=249284

这个结果还是比目标小，取区间[0.0425，0.045]的中间点I3＝(0.0425+0.045)/2＝0.04375，进行计算，结果如下：

[12*200/0.04375][(1 + 0.04375/12)^420]=252952

结果又有些高，因此取中间值I4＝(0.0425+0.04375)/2＝0.043125，进行计算如下：

[12*200/0.043125][(1 + 0.043125/12)^420]=251085

结果还高，继续取中间值I5＝(0.0425+0.043125)/2＝0.0428125，进行计算如下：

(12*200/0.0428125)((1 + 0.0428125/12)^420)=250176

如果还需要更多的有效位数，可进行进一步的迭代。这个例子的目的是对特定的L寻找I，使得A(I)＝L。将常量L放在左边并求解A(I)－L＝0是一个标准的方法。

注意：（1）对分法只能找到f(x)＝0的一个根，因此它仅适用于单数重实根的情形。

    （2）若f(x)[a，b]，但f(a)f(b)＞0，不表明f(x)＝0没有根，这时对分法失效。

 

 

3.1.5     试位(值)法

 

另一个常用的算法是试位(值)法，由于二分法收敛速度相对较慢，因此试位(值)法对它进行了改进。与上述条件一样，假设与符号相反。二分法使用区间的中点进行下一次迭代。如果找到经过点和      的割线L与x轴的交点c，如下图所示，则可能得到一个更好的近似值c。

要寻找c，需定义线L的斜率k的两种表示，一种表示为：,

这里使用了点和；另一种表示为：，这里使用了点和。由斜率相等，则有：。

从中解出c，可得：。

会出现三种与前面类似的可能性：

① 如果和符号相同，则在区间内存在零点；

② 如果和符号相同，则在区间内存在零点；

③ 如果0，则是零点。

    试位(值)法的收敛性和二分法类似。结合①、②两种情况，表示的判定过程可构造区间序列，其中的每个序列包含零点。在每一步中，零点r的近似值为：

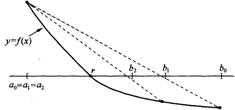而且可以证明序列{cn}将收敛到零点r。但要注意，尽管区间宽度越来越小，但它可能不趋近于0。例如曲线函数y＝(x)在靠近点(r，0)处是凹形，一个端点固定，另一个点逼近解，但区间不趋近于零，如右图所示。

    【例3.1.4】利用试位(值)法求解xsinx－l＝0在区间[0，2]内的根，并观察它是否比二分法收敛得快。

解  初始值＝0，b0＝2。计算：(0)＝－1.000000和(2)＝0.818595，因此，(x)＝0的一个根位于区间[0，2]内。

计算c0＝21.099750，(c0)＝－0.0200193，所以从左边压缩令＝c0＝1.099750，b1＝b0＝2，则(x)区间[，]＝[1.099750，2]内有根。

计算c1＝21.121240，(c1)＝0.0098346，所以从右边压缩，令＝＝1.099750，b2＝c1＝1.121240，则(x)区间[，]＝[1.099750，1.121240]内有根。

计算c2＝1.1212401.114161，

(c2)＝(4.93352767)×10-6≈0.00000493，同理，f(x)在区间[，]＝[1.099750，1.114161] 内有根(从右边压缩)。

计算c3＝1.1141611.11415745

(c3)＝(4.3207940780831677)×10-7≈0.00000043≈0

可见试位(值)法比二分法收敛得快。