§3.2 简单迭代法
迭代法是一种逐次逼近的方法,其基本思想是利用某种递推算式,使某个预知的近似根(简称初值)逐次精确化,从而得到一个近似根序列,使得该近似根序列的极限就是方程的根。
对非线性方程f(![]() )=0,用简单迭代法求根的具体做法是:
)=0,用简单迭代法求根的具体做法是:
设函数f(![]() )在有根区间上连续,将方程f(x)=0改写成等价形式:
)在有根区间上连续,将方程f(x)=0改写成等价形式:![]() =
=![]() ,例如,最简单的可取
,例如,最简单的可取![]() =
=![]() 。然后取初始值
。然后取初始值![]() ,计算
,计算![]() =
=![]() ,
,![]() 0,1,2,…,可得一序列{
0,1,2,…,可得一序列{![]() }。这种方法称为迭代法(或简单迭代法),称
}。这种方法称为迭代法(或简单迭代法),称![]() 为迭代函数。如果
为迭代函数。如果![]() 连续,且序列{
连续,且序列{![]() }收敛到
}收敛到![]() ,则有:
,则有:
![]()
即![]() 满足方程
满足方程![]() =
=![]() ,而方程
,而方程![]() =
=![]() 与方程f(
与方程f(![]() )=0等价,所以
)=0等价,所以![]() 就是方程f(
就是方程f(![]() )=0的一个根。此时称该迭代法收敛;否则称迭代法发散。
)=0的一个根。此时称该迭代法收敛;否则称迭代法发散。
迭代法的几何意义可解释为:求方程![]() =
=![]() 的根
的根![]() ,在几何上就是求直线y=x与曲线y=
,在几何上就是求直线y=x与曲线y=![]() 交点P*的横坐标,见下图。
交点P*的横坐标,见下图。
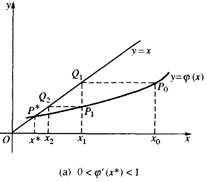
对于![]() 的某个初始近似值x0,对应于曲线y=
的某个初始近似值x0,对应于曲线y=![]() 上一点P0(x0,
上一点P0(x0,![]() ),过P0点引平行于x轴的直线,交直线y=x于点Q1(x1,x1),过Q1再作平行于y轴的直线,它与曲线y=
),过P0点引平行于x轴的直线,交直线y=x于点Q1(x1,x1),过Q1再作平行于y轴的直线,它与曲线y=![]() 的交点记作P1(x1,
的交点记作P1(x1,![]() );过AP1再作平行于x轴的直线,又交直线y=x于点Q2(x2,x2),…。继续如此做下去,就在曲线y=
);过AP1再作平行于x轴的直线,又交直线y=x于点Q2(x2,x2),…。继续如此做下去,就在曲线y=![]() 上得到点列P0,P1,P2,…,逐渐逼近于曲线y=
上得到点列P0,P1,P2,…,逐渐逼近于曲线y=![]() 与直线y=x的交点P*,点列的横坐标x0,x1,x2,…,逐渐趋于根
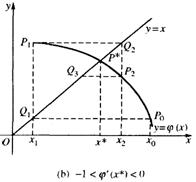
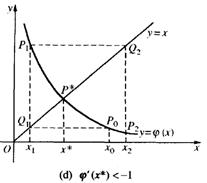
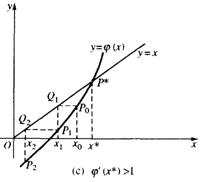
与直线y=x的交点P*,点列的横坐标x0,x1,x2,…,逐渐趋于根![]() 。可见,此时迭代格式收敛,如下图中的(A),(B),否则迭代格式发散,如下图中的(C),(D)。
。可见,此时迭代格式收敛,如下图中的(A),(B),否则迭代格式发散,如下图中的(C),(D)。
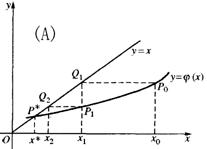
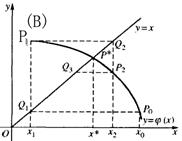
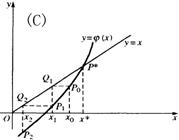
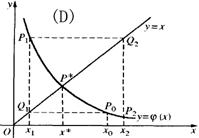
从图中可知,当迭代函数满足不同条件时,迭代过程的收敛情况也有所不同。由此可见,迭代过程的收敛依赖于迭代函数的构造,为使迭代法有效,必须保证它的收敛性,一个产生发散序列的迭代函数是没有任何使用价值的。
设![]() 为连续函数,且
为连续函数,且![]() ,则
,则![]() 。故
。故![]() 是方程
是方程![]() 的解,称
的解,称![]() 为迭代函数的不动点,故简单迭代法又称为不动点迭代法。
为迭代函数的不动点,故简单迭代法又称为不动点迭代法。
上述这种迭代法,是从一个初始近似值x0出发计算迭代的,一般也称为单点迭代法,由迭代产生的数列{![]() }称为迭代序列。显然,迭代函数
}称为迭代序列。显然,迭代函数![]() 依赖于函数f(x),用不同的方法构造迭代函数就得到不同的迭代方法。
依赖于函数f(x),用不同的方法构造迭代函数就得到不同的迭代方法。
但是要注意,迭代法的效果并不总是令人满意的,迭代过程可能收敛,也可能发散,就是同一个方程,当取不同迭代格式时也会得到完全不同的效果。
【例
解 把方程分别改写成下列三种等价的便于迭代的形式:
⑴ ![]() =16-
=16-![]() ;⑵
;⑵ ![]() ;⑶
;⑶ ![]()
若取相同的初值x0=3,分别迭代计算得到的结果列于下表:
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
x(1) |
3 |
7 |
-33 |
-1073 |
-1151313 |
|
|
|
|
|
x(2) |
3 |
4 |
3.2 |
3.810 |
3.326 |
3.699 |
3.405 |
3.632 |
3.454 |
|
x(3) |
3 |
3.571 |
3.531 |
|
|
|
|
|
|
已知方程的一个根是3.531。从表中数据的变化趋势看,迭代格式x(1)得到的序列是发散的;迭代格式x(2)得到的序列虽然收敛,但收敛速度很慢;迭代格式x(3)得到的序列不但收敛,而且收敛速度很快。
 【例
【例![]() =0的根。
=0的根。
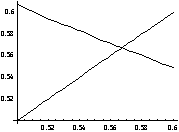
解:将方程分解为迭代形式:![]()
图形![]() 与
与![]() 交点的横坐标
交点的横坐标![]() 在区间
在区间
![]() 内,取初值
内,取初值![]() ,按迭代公式:
,按迭代公式:![]() 计算数据如下:0.5000 0.6065 0.5452 0.5797 0.5601 0.5712 0.5649 0.5684 0.5664 0.5676 0.5669 0.5673 0.5671 0.5672 0.5671 0.5672 0.5671 0.5671
计算数据如下:0.5000 0.6065 0.5452 0.5797 0.5601 0.5712 0.5649 0.5684 0.5664 0.5676 0.5669 0.5673 0.5671 0.5672 0.5671 0.5672 0.5671 0.5671
从上述计算可以看出,迭代函数选取的不同,相应的迭代序列的收敛情况也不一样,即使同是收敛的迭代格式,也有一个速度快慢的问题。对于一个发散的迭代过程,纵使进行千百次迭代,其结果也是毫无价值的。迭代法的敛散性关键取决于迭代函数在有根区间内的性态。首先,迭代函数必须使由初始值x0产生的迭代序列{![]() },满足{
},满足{![]() }
}![]() ,(迭代函数的定义域);其次,从迭代法的几何意义图上看到,函数曲线变化比较缓慢是迭代收敛的良好征兆。图中收敛的情况,其共同特征是曲线走势比较平坦,而发散的共同特征是曲线走势很陡峭。
,(迭代函数的定义域);其次,从迭代法的几何意义图上看到,函数曲线变化比较缓慢是迭代收敛的良好征兆。图中收敛的情况,其共同特征是曲线走势比较平坦,而发散的共同特征是曲线走势很陡峭。
定义![]() 都有
都有![]() ,且对任意的x,y
,且对任意的x,y![]() 有:
有:![]()
其中0<L<l,则称![]() 是区间
是区间![]() 上的压缩映象,数L称为压缩系数。
上的压缩映象,数L称为压缩系数。
例如,![]() 就是区间
就是区间![]() 上的压缩映象,因为:
上的压缩映象,因为:
![]()
这时压缩系数为![]() 。由此定义还可以得出,区间
。由此定义还可以得出,区间![]() 上的压缩映象
上的压缩映象![]() ,一定是区间
,一定是区间![]() 上的连续函数。
上的连续函数。
若![]() 是压缩映象,则
是压缩映象,则![]()
![]() 一定有唯一的不动点,这就是著名的压缩映象原理。
一定有唯一的不动点,这就是著名的压缩映象原理。
定理![]() 是有限区间
是有限区间![]() 上的压缩映象,则:
上的压缩映象,则:
⑴ 函数![]() 在
在![]() 上有唯一的不动点
上有唯一的不动点![]() ;
;
⑵ 对任何迭代初值![]()
![]() ,不动点迭代
,不动点迭代![]() =
=![]() 收敛于不动点
收敛于不动点![]() ,即
,即![]()
![]() ;
;
⑶ 迭代n次的误差估计式有:① ![]()
② ![]()
其中L为压缩系数。误差估计式②称为事后估计,它常常作为上机计算时的停机标准,这种误差估计也叫做实用估计;误差估计式①称为先验估计式,根据给定的误差要求,可估计出计算的步数k,由①式可以得出以下估计式:
![]()
![]()
![]() ,两边取对数得:
,两边取对数得:![]()
由于0<L<l,所以![]() ,则可得:
,则可得: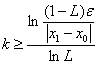
应用压缩映象原理判断不动点迭代的收敛性的关键在于找到小于1的正数L作为压缩系数,寻找这样的L比较困难,下面的推论以条件![]() <1代替条件O<L<1。
<1代替条件O<L<1。
推论 设迭代函数![]() ,并且在区间
,并且在区间![]() 上有
上有![]() <1,则定理
<1,则定理
由迭代格式的几种图形中,可以清楚地看出,当导数![]() 时,迭代法单调收敛;当导数
时,迭代法单调收敛;当导数![]() 时,迭代法振荡收敛;当导数
时,迭代法振荡收敛;当导数![]() 时,迭代法单调发散;当导数
时,迭代法单调发散;当导数![]() 时,迭代法振荡发散。
时,迭代法振荡发散。