§3.3 加速技术
3.3.1 收敛速度
一种迭代法具有实用价值,不仅需要肯定它是收敛的,还要求知道它的收敛速度。关于收敛速度,我们有如下定义:
定义![]() }收敛于
}收敛于![]() ,令
,令![]() ,设当
,设当![]() 时有:
时有:
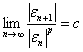 ,(c为大于零的常数)
公式(
,(c为大于零的常数)
公式(
则称迭代过程是![]() 阶收敛。
阶收敛。
当![]() =1,c<1时称为线性收敛;
=1,c<1时称为线性收敛;![]() =2时称为二阶收敛(或为称平方收敛),1<
=2时称为二阶收敛(或为称平方收敛),1<![]() <2时称为超线性收敛。
<2时称为超线性收敛。
定理![]() 在方程
在方程![]() 的根
的根![]() 邻近有连续的导函数,则当
邻近有连续的导函数,则当![]() <1,且
<1,且![]() 时,迭代过程
时,迭代过程![]() 为线性收敛;而当
为线性收敛;而当![]() ,
,![]() 时为二阶收敛。
时为二阶收敛。
一般来说,若![]() ,而
,而![]() ,称迭代过程
,称迭代过程![]() 在
在![]() 附近为
附近为![]() 阶收敛。
阶收敛。
从![]() =0构造出的迭代格式
=0构造出的迭代格式![]() 可能不收敛;另外在收敛时,收敛的速度取决于
可能不收敛;另外在收敛时,收敛的速度取决于![]() 的大小,当
的大小,当![]() 接近于1时,收敛可能很慢,这两种情况都影响迭代法的应用。能否从出发构造出新的迭代形式,使其收敛速度加快呢?下面介绍几种常用的加速技术。
接近于1时,收敛可能很慢,这两种情况都影响迭代法的应用。能否从出发构造出新的迭代形式,使其收敛速度加快呢?下面介绍几种常用的加速技术。
3.3.2 参数法
1从迭代格式![]() 出发,两边同时减去
出发,两边同时减去![]() ,得到一个与
,得到一个与![]() 等价的方程:
等价的方程:![]() ,当
,当![]() 和
和![]() 时,上式化为:
时,上式化为:![]() ,
,
设![]()
![]() ,选择适当的参数
,选择适当的参数![]() ,使
,使![]() 尽可能地小。因为
尽可能地小。因为![]()
![]() ,显然取
,显然取![]() 时(
时(![]() ),比较合适。据此选定的
),比较合适。据此选定的![]() 便可建立迭代公式:
便可建立迭代公式:![]() ,(
,(![]() )。 公式(
)。 公式(
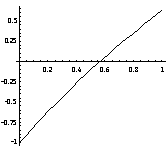 【例
【例![]()
解:由图解法可知方程的解![]() [0.4,0.6],而
[0.4,0.6],而
![]()
可取![]() ,建立以下迭代公式:
,建立以下迭代公式:
![]()
取初值![]() ,(Exp[-0.5] + 0.6*0.5)/1.6 Out=0.566582
,(Exp[-0.5] + 0.6*0.5)/1.6 Out=0.566582
(Exp[-0.5665816623203959`] + 0.6*(0.5665816623203959`))/1.6 Out=0.567132
(Exp[-0.5671318130420451`] + 0.6*(0.5671318130420451`))/1.6 Out=0.567143
(Exp[-0.567143054740294`] + 0.6*(0.567143054740294`))/1.6 Out=0.567143
2 我们也可以从方程![]() 出发来构造出新的等价的方程:
出发来构造出新的等价的方程:
![]()
选择适当的参数![]() ,使
,使![]() ,以达到收敛的目的。由上式可见,
,以达到收敛的目的。由上式可见,![]() 值的选取与
值的选取与![]() 的大小有关,为此,先对
的大小有关,为此,先对![]() 在区间[
在区间[![]() ,
,![]() ]内的值做出以下的估计:
]内的值做出以下的估计:![]() 。这里假设
。这里假设![]() >0,若
>0,若![]() <0时,可对原方程乘以负号就可化成上述情况。为了使
<0时,可对原方程乘以负号就可化成上述情况。为了使![]() ,就必须选择适当的参数
,就必须选择适当的参数![]() ,同时满足
,同时满足![]() 与
与![]() 。从两个不等式中解出
。从两个不等式中解出![]() 的取值范围为:
的取值范围为:![]() 及
及![]() 。由
。由![]() 的表达式可以看出,若取
的表达式可以看出,若取![]() ,
,
可获得较小的![]() 值,通常可取
值,通常可取![]() ,则
,则![]() 。
。
显然,0<![]() <
<![]() ,0<
,0<![]() <
<![]() ,则相应的迭代公式为:
,则相应的迭代公式为:
![]() ,(
,(![]() )。 公式(
)。 公式(
【例![]() 。
。
解:由图象可知,![]() 。
。![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,代入公式(
,代入公式(
![]()
![]()
取![]() ,计算得:0.5000 0.5675 0.5672 0.5672
,计算得:0.5000 0.5675 0.5672 0.5672
3 如果把![]() 改写为:
改写为:
![]() 公式(
公式(
并与公式(![]() 比较,可知
比较,可知![]() 与
与![]() 间有以下关系:
间有以下关系:![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() 。可见公式(3.3.2)与公式(3.3.4)两者之间可以相互转换。
。可见公式(3.3.2)与公式(3.3.4)两者之间可以相互转换。
公式(![]()
若令![]() ,上式可改写为:
,上式可改写为:![]()
它实际上就是相邻两个迭代值![]() 与
与![]() 按
按![]() 与
与![]() 之比的组合公式。如取
之比的组合公式。如取![]() =1/2,就得到以下迭代公式:
=1/2,就得到以下迭代公式: 公式(
公式(
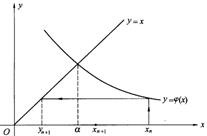 它取相邻两个迭代值的算术平均值作为新的近似值,如右图所示。当迭代序列中的各次近似值在根的两侧往复地趋近于根
它取相邻两个迭代值的算术平均值作为新的近似值,如右图所示。当迭代序列中的各次近似值在根的两侧往复地趋近于根![]() 时,使用公式(
时,使用公式(
【例
![]() 。
。
解 取初值![]() ,按公式(
,按公式(
0.5000 0.5533 0.5642 0.5665 0.5670 0.5671 0.5671
从迭代格式![]() 中,我们知道
中,我们知道![]() 与
与![]() 同是
同是![]() 的近似值,那么:
的近似值,那么:
![]()
是两个近似值的加权平均,其中![]() 称为权重,现通过选择适当的
称为权重,现通过选择适当的![]() ,看能否得到加速的迭代格式。写出迭代方程:
,看能否得到加速的迭代格式。写出迭代方程:![]() ,令:
,令:
![]()
试确定权重![]() 。当
。当![]() 时,有
时,有![]() ,即当
,即当![]() 时,可望获得较好的加速效果,于是有松弛法公式:
时,可望获得较好的加速效果,于是有松弛法公式:
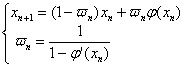 公式(
公式(
松弛法的加速效果是明显的,甚至有一些不收敛的迭代函数,经过使用松弛法加速后也能获得收敛的效果。
3.3.4 艾特肯(Altken)方法
艾特肯加速迭代公式的来源有以下几种方式:
1 在松弛法中,要先算![]() ,在使用中及不方便,为此研究出以下的艾特肯公式。设迭代格式为:
,在使用中及不方便,为此研究出以下的艾特肯公式。设迭代格式为:![]() ,
,![]() 是一个初始值,
是一个初始值,![]() 是它的根。
是它的根。
设![]() ,
,![]() ,因为
,因为![]()
用差商![]() ,近似代替
,近似代替![]() ,有:
,有:
![]()
解出![]() 得:
得:![]() ,由此可得到艾特肯加速迭代公式:
,由此可得到艾特肯加速迭代公式:
 公式(
公式(
2 为了获得较好的参数值,Aitken(1931年)和Steffensen(1933年)分别设计出求取参数值的相同方法,现叙述如下。
首先将方程![]() 分解为迭代形式
分解为迭代形式![]() ,然后由
,然后由![]() 出发,迭代两次得到三个相邻的迭代值:
出发,迭代两次得到三个相邻的迭代值:![]() ,
,![]() ,
,![]() 。取以下平均变化率作为参数值
。取以下平均变化率作为参数值![]() :
:![]() 。代入公式(
。代入公式(
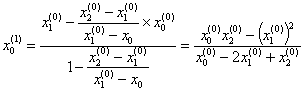
在求得![]() 的基础上,继续求三个相邻迭代值:
的基础上,继续求三个相邻迭代值:![]() ,
,![]() ,
,![]() 。仍取平均变化率作为参数值
。仍取平均变化率作为参数值![]() :
:![]() 。代入公式(
。代入公式(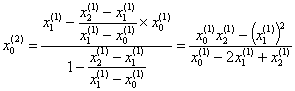 。
。
以此类推,其一般公式可归纳为: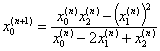 。 公式(
。 公式(
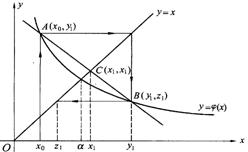 这个方法叫做爱特肯——斯蒂芬森加速收敛法。Willers(1948年)给出了它的几何解释。见右图。按照本法的计算过程,由
这个方法叫做爱特肯——斯蒂芬森加速收敛法。Willers(1948年)给出了它的几何解释。见右图。按照本法的计算过程,由![]() 出发,通过一次迭代得到
出发,通过一次迭代得到![]() ,这样便在曲线
,这样便在曲线![]() 上得到点A(
上得到点A(![]() ,
,![]() );再迭代一次得
);再迭代一次得![]() ;又可在曲线
;又可在曲线![]() 上得到点B(
上得到点B(![]() ,
,![]() )。联结A、B两点得到直线AB,设此直线与
)。联结A、B两点得到直线AB,设此直线与![]() 直线的交点为C(
直线的交点为C(![]() ,
,![]() )点,则A、B、C点坐标同在直线方程上,斜率相等即得:
)点,则A、B、C点坐标同在直线方程上,斜率相等即得:![]() ,解出
,解出![]() ,可得:
,可得:
![]() 。
。
它与公式(![]() ,求与
,求与![]() 交点的迭代方法。
交点的迭代方法。
3 设迭代序列{![]() }线性地收敛于
}线性地收敛于![]() ,即:
,即: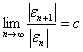 ,(
,(![]() ),
),
可按如下方法由序列{![]() }构造一个比它更快地收敛于
}构造一个比它更快地收敛于![]() 的序列{
的序列{![]() }。首先假定
}。首先假定![]() 均同号,则有近似关系式:
均同号,则有近似关系式:![]() ,
,![]() 。
。
由这两式消去c得:![]()
解出![]() ,得:
,得:![]()
![]()
![]()
设左端的近似值为![]() ,则
,则![]()
![]() 。
。
即可以得到艾特肯公式,它是利用已求得的![]() 、
、![]() 和
和![]() 作修正得到比
作修正得到比![]() 更精确的值
更精确的值![]() ,这一修正加速了迭代的收敛,序列{
,这一修正加速了迭代的收敛,序列{![]() }的收敛速度是{
}的收敛速度是{![]() }的两倍。艾特肯方法可以应用于本章介绍的各种迭代格式。
}的两倍。艾特肯方法可以应用于本章介绍的各种迭代格式。
艾特肯加速算法的步骤是:⑴ 给定迭代初值![]() ;⑵ 迭代计算
;⑵ 迭代计算![]() ,
,![]() ,…,
,…,![]() ;⑶ 应用艾特肯加速公式,由
;⑶ 应用艾特肯加速公式,由![]() ,
,![]() ,
,![]() 算出
算出![]() 。将以上步骤稍加改进就成为Steffensen算法。它是由初值
。将以上步骤稍加改进就成为Steffensen算法。它是由初值![]() 迭代两次得
迭代两次得![]() ,
,![]() ,再由
,再由![]() ,
,![]() ,
,![]() ,应用艾特肯公式加速公式得到
,应用艾特肯公式加速公式得到![]() ,立即用
,立即用![]() 进行迭代得
进行迭代得![]() ,
,![]() ,再加速得
,再加速得![]() ,以此类推。其步骤是:
,以此类推。其步骤是:
⑴ 给出选代初值![]() ;⑵ 迭代计算
;⑵ 迭代计算![]() ,
,![]() ;
;
⑶ 应用艾特肯加速公式,由![]() ,
,![]() ,
,![]() 计算出
计算出![]() 。
。
【例![]() 。
。
解:取![]() ,则
,则![]() ,
,![]() ≈0.545239。进而可计算:
≈0.545239。进而可计算:![]() 。
。
接着计算:![]() ,
,![]() 。
。
![]() ,
,![]() ,
,![]() 。
。
艾特肯加速迭代法的加速效果也是十分明显的,使用艾特肯加速迭代法的加速技术后,可能使某些不收敛的迭代格式获得收敛的效果。
斯蒂芬森加速迭代技术中的条件只是![]() ,而当
,而当![]() 时,不动点迭代
时,不动点迭代![]() 是线性收敛的,当
是线性收敛的,当![]() 时,不动点迭代是不收敛的,但在两种情形都有
时,不动点迭代是不收敛的,但在两种情形都有![]() ,斯蒂芬森迭代却是二阶收敛的,所以迭代函数由不动点迭代
,斯蒂芬森迭代却是二阶收敛的,所以迭代函数由不动点迭代![]() 改为斯蒂芬森迭代,不但能改进收敛速度,有时也能把不收敛的迭代改进为收敛的二阶迭代方法,这是很了不起的。
改为斯蒂芬森迭代,不但能改进收敛速度,有时也能把不收敛的迭代改进为收敛的二阶迭代方法,这是很了不起的。
严格来讲,艾特肯加速技术可对线性收敛的序列进行加速,不管这个序列是如何得来的。此时的加速公式为:![]()
![]() 。
。
可以证明,序列{![]() }比{
}比{![]() }较快地收敛于极限
}较快地收敛于极限![]() 。只有对由不动点迭代产生的序列应用艾特肯加速技术时,得到的迭代公式才叫斯蒂芬森迭代。
。只有对由不动点迭代产生的序列应用艾特肯加速技术时,得到的迭代公式才叫斯蒂芬森迭代。
从上述计算结果可以看出,斯蒂芬森迭代技术的加速收敛效果确实是非常显著的,特别是将原来不收敛的迭代经过加速技术后变得收敛,且只要![]() ,在
,在![]() 的邻近就是二阶收敛的。需要指出的,斯蒂芬森加速技术一般不对高阶收敛的迭代法进行加速,因为此时的加速效果不明显。
的邻近就是二阶收敛的。需要指出的,斯蒂芬森加速技术一般不对高阶收敛的迭代法进行加速,因为此时的加速效果不明显。