§4.1 插值的基本概念

4.1.1 代数插值问题的提法

我们知道，许多实际问题都可用函数来表示变量间的某种内在规律的数量关系，但是，在工程技术与科学研究中，有时对函数只能通过实验或观测等手段得到它在某区间上的有限个不同点上的函数值 ，即只知道一张函数表，却没有明确的函数表达式；有时，虽然函数有明确的解析表达式，但由于形式复杂，不便于计算和使用，通常宁可先在某些点上取值后造一张函数表。为了从给定的函数表进一步研究函数的性质，人们往往希望作出一个既能反映函数的特性，又便于计算的简单函数去近似代替，并且还要求满足条件：，，则称这类问题为插值问题，称为插值函数。

特别以代数多项式作为插值函数的插值问题称为代数插值，这种插值函数叫做代数插值多项式，简称插值多项式。本章中仅分析代数插值，而这方面的研究，无论是对实际应用还是对计算领域本身都是极其重要的。

定义4.1.1 设函数在区间上连续，且已知它在区间上个互异点，…，上的函数值，若存在一个次数不超过n次的多项式：，（其中为实数）

满足条件：， （4.1.1）

则称为函数在结点处的n次代数插值多项式。相应的插值问题称为n次代数插值问题，求插值函数的方法称为插值法。点称为插值结点或简称为结点，函数称为被插值函数，条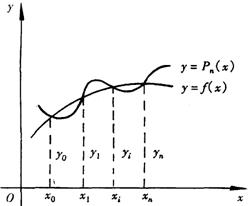件（4.1.1）称为插值条件，被称为插值区间，点称为插值点。插值点在插值区间内的叫做内插，否则称为外插。

代数插值有明确的几何意义，就是通过平面上给定的个互异点，作一条次数不超过n次的代数曲线＝去近似地表示曲线。如图所示。

4.1.2 插值多项式的存在唯一性

现在的问题是，满足插值条件（4.1.1）的多项式是否存在？如果存在，则有多少？回答是肯定的。由插值条件易知，插值多项式的系数，，…，应满足如下线性方程组：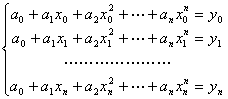

其系数行列式便是一个n＋1阶范德蒙（Vandermonde）行列式D。由线性代数理论知：，因结点互异，故D≠0，方程组有唯一解。于是有：

定理4.1.1 当n+1个插值结点互异时，满足插值条件（4.1.1）而次数不超过n的插值多项式存在并且唯一。

定理4.1.1说明，不论用什么方法来构造，也不论用什么形式来表示插值多项式，只要满足同样的插值条件（4.1.1）其结果都是互相恒等的。

【例4.1.1】已知三点A(－1，1)，B(1，1)和C(2，1)，求过这三点的插值多项式，并求时的函数值。

解：通过三点A，B和C的二次插值多项式：

将三点处的值代入，可得方程组：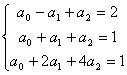

解得：

则所求的二次插值多项式：

当时，

4.1.3 插值余项

由插值条件可以看出，用插值多项式近似代替，除了在插值结点处的函数值没有误差外，在其它点一般都有误差。若记：，

则称为用插值多项式近似代替的截断误差。并称为n次插值多项式的余项，其值可由下面定理来估计。

定理4.1.2 若函数在区间上有直到n＋1阶的导数，是在n+1个结点处的n次插值多项式，则对任何有余项公式： （4.1.2）

其中，且依赖于x的取值。

插值问题的关键，是怎样具体去求插值多项式。事实上，从存在唯一性定理出发，亦提供了一种构造插值多项式的一种求法，即通过解线性方程组来确定其系数，但这样做当n较大时，不但计算工作量大，而且因不能获得简明实用的表达式给理论研究与应用带来不便，因而利用解方程组的方法去构造插值多项式是不实用的。然而，既然已经证明插值多项式是唯一存在的，那么就可以利用其它行之有效的方法来构造实用的插值多项式。下面分别介绍几种简便而实用的构造代数插值多项式的方法。