§4.2 Lagrange插值方法
4.2.1 拉格朗日插值多项式的基本概念
1
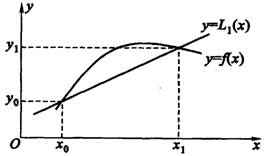
线性插值
由存在性唯一性定理的证明过程可知,每一个代数插值问题实质上对应一个线性代数方程组的求解问题。对于插值方法的研究实际上是围绕插值条件所引出的线性方程组的求解方法的研究来展开的。常用的方法是插值基函数方法,具有代表性的基函数是拉格朗日基函数,由此而构造的插值多项式称为拉格朗日插值多项式。首先来讨论拉格朗日插值方法的线性插值。
 已知数据(
已知数据(![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
求满足插值条件:![]() ,
,
![]() 的线性插值函数:
的线性插值函数:
![]() 。
。
从几何上看,![]() 的图形是通过平面上两个定点的直线。由直线的点斜式方程(也可以用两点式方程),所求线性插值函数可表示为:
的图形是通过平面上两个定点的直线。由直线的点斜式方程(也可以用两点式方程),所求线性插值函数可表示为:
![]() 。
(
。
(
【例![]() 的值。
的值。
解 常用的正弦函数特殊值有:![]() ,
,![]() ,
,![]() ,
,
⑴取![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,利用公式(
,利用公式(
![]()
⑵ 若取![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,利用公式(
,利用公式(
![]()
这个数较好的接近于正弦函数在该点的值0.5878(取小数点后四位)。
为了将两点插值公式推广到多点插值问题,公式(
![]() (
(
上式被称为拉格朗日线性插值函数。在这一表达式中,![]() 是两个函数值
是两个函数值![]() 和
和![]() 的线性组合,组合系数是两个线性函数:
的线性组合,组合系数是两个线性函数:![]() ,
,![]() ,并且
,并且![]() 。
。
通常,我们称![]() 与
与![]() 为拉格朗日线性插值基函数。插值基函数在插值节点处满足条件:
为拉格朗日线性插值基函数。插值基函数在插值节点处满足条件:![]()
即:![]() ,
,![]() ,
,![]() ,
,![]() 。
。
公式(
【例![]() ,
,![]() ,计算
,计算![]() 。
。
解取![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,利用公式(
,利用公式(
![]()
所以![]() 。(查表可得
。(查表可得![]() 2.6458)
2.6458)
2
抛物插值
若已知数据为:(![]() ,
,![]() ),(
),(![]() ),求满足插值条件
),求满足插值条件![]() ,
,![]() ,
,![]() 的二次插值函数
的二次插值函数![]() 。由线性插值的启示及拉格朗日插值公式的特点,可令:
。由线性插值的启示及拉格朗日插值公式的特点,可令:![]()
其中![]() ,(
,(![]() ),为二次多项式,并满足:
),为二次多项式,并满足:
![]() (
(
称![]() ,(
,(![]() ),为二次拉格朗日插值基函数。
),为二次拉格朗日插值基函数。
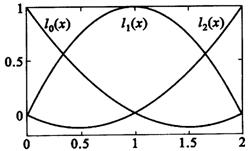 由于每个插值基函数的零点都是插值结点,利用待定系数法及零点原理可以写出三个插值基函数。以
由于每个插值基函数的零点都是插值结点,利用待定系数法及零点原理可以写出三个插值基函数。以![]() 为例,由公式(
为例,由公式(![]() 与
与![]() 为
为![]() 的两个零点,故应有
的两个零点,故应有![]() ,而在
,而在![]() 处,
处,![]() 的值为1。所以
的值为1。所以![]() ,则
,则![]() ,同理可得:
,同理可得:![]() ,
,![]()
这三个插值基函数是与插值结点有关的二次函数,同样满足:
![]() ≡1。若取
≡1。若取![]() =0,
=0,![]() ,
,![]() =2,可绘制出三个基函数在区间[0,2]上的图形。所以,拉格朗日二次插值函数为:
=2,可绘制出三个基函数在区间[0,2]上的图形。所以,拉格朗日二次插值函数为:
![]()
![]()
![]()
![]()
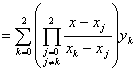 (
(
【例![]() ,
,![]() ,
,![]() ,计算
,计算![]() 。
。
解取![]() ,
,![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,利用公式(
,利用公式(
![]()
所以![]() 。(查表可得
。(查表可得![]() 2.6458)
2.6458)
与![]() 的准确值相比较,可以发现
的准确值相比较,可以发现![]() 比
比![]() 的误差小。这就需要考虑两个问题:① 通常准确值是不知道的,如何估计误差?② 是不是插值多项式的次数越高,结果越精确?后面要专门讨论这两个问题。
的误差小。这就需要考虑两个问题:① 通常准确值是不知道的,如何估计误差?② 是不是插值多项式的次数越高,结果越精确?后面要专门讨论这两个问题。
【例![]() ,
,![]() ,
,![]() ,
,![]() ,试选用合适的插值结点,利用二次插值多项式计算
,试选用合适的插值结点,利用二次插值多项式计算![]() 的近似值,使其有尽可能高的精度。
的近似值,使其有尽可能高的精度。
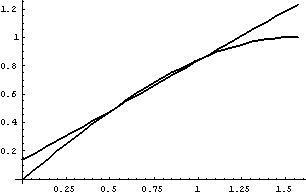
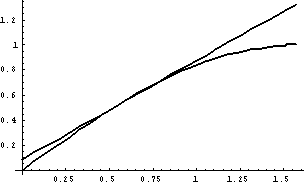
解 ⑴ 选x0=-1,x1=0,x2=0.5为插值节点,拉格朗日插值基函数为:
l0(x)=![]() =
=![]() =
=![]() x(x-0.5)
x(x-0.5)
l1(x)=![]() =
=![]() =-2(x+1)(x-0.5)
=-2(x+1)(x-0.5)
l2(x)=![]() =
=![]() =
=![]() x(x+1)
x(x+1)
二次插值多项式为:L2(x)=l0(x)y0+l1(x)y1+l2(x)y2
=![]() y0+
y0+![]() y1+
y1+![]() y2
y2
=l0(x)+2l1(x)+3l2(x),
于是:f(-0.5)≈L2(-0.5)=l0(-0.5)+2l1(-0.5)+3l2(-0.5)=4/3。
⑵ 选x0=-2,x1=-1,x2=0为插值节点,拉格朗日插值基函数为:
l0(x)=![]() =
=![]() =
=![]()
l1(x)=![]() =
=![]() =-
=-![]()
l2(x)=![]() =
=![]() =
=![]()
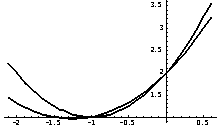 二次插值多项式为:
二次插值多项式为:
L2(x)=l0(x)y0+l1(x)y1+l2(x)y2
=2l0(x)+l1(x)+2l2(x)
于是:f(-0.5)≈L2(-0.5)
=2l0(-0.5)+l1(-0.5)+
2l2(-0.5)=1.25。
两个二次插值函数图形见右图。
若用程序ldk421做三次插值,结果如下:
x0=[-2 -1 0
0.5];y0=[2 1 2 3];
x1=-0.5;ldk421(x0,y0,x1)
ans = 1.3000
3
n次插值
由线性代数的基本理论,所有不高于n次的代数多项式全体组成一个n+1维线性空间,其基有各种不同的取法。如果取满足条件:![]()
(![]() )的一组n次代数多项式作为上述线性空间的基(读者试证明,满足上述条件的一组代数多项式必定线性无关),则容易看出:
)的一组n次代数多项式作为上述线性空间的基(读者试证明,满足上述条件的一组代数多项式必定线性无关),则容易看出:
![]() (
(
必定是一个次数不高于n次的代数多项式,而且它在结点![]() ,
,![]() …,
…,![]() 上的值依次为
上的值依次为![]() ,
,![]() ,…
,…![]() 。也就是说,由n+1个n次代数多项式
。也就是说,由n+1个n次代数多项式![]() ,
,![]() ,…
,…![]() 线性生成的多项式(
线性生成的多项式(
n次代数多项式![]() ,称为n次拉格朗日插值基函数,由此构造出的多项式(
,称为n次拉格朗日插值基函数,由此构造出的多项式(![]() 。与计算二次拉格朗日插值基函数的方法类似,利用待定系数法及零点原理可以求出n次拉格朗日插值基函数的表达式:
。与计算二次拉格朗日插值基函数的方法类似,利用待定系数法及零点原理可以求出n次拉格朗日插值基函数的表达式:
![]() ,
,![]()
则n次拉格朗日插值多项式可写成以下形式:![]()
=![]() =
=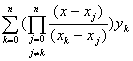 (
(
【例![]() ,
,![]() ,
,![]() 的值。
的值。
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
12 |
234 |
34 |
-1 |
34 |
2 |
5 |
23 |
34 |
9 |
45 |
23 |
解:利用MATLAB程序ldk421,计算出结果:
x=[1:12];fx=[12 243
34 -1 34 2 5 23 34 9 45 23];
x3=[6.5 7.2
11.5];ldk421(x,fx,x3)
f = -2.5590 9.3943 236.6987
4
拉格朗日插值多项式的性质
定理![]() ,
,![]() …,
…,![]() 为n+1个互异的结点,
为n+1个互异的结点,![]() 为拉格朗日n次基本插值多项式,则有以下结论:⑴
为拉格朗日n次基本插值多项式,则有以下结论:⑴ ![]()
⑵ ![]()
⑶ 设![]() 为任意一个首1的n+1次多项式,则:
为任意一个首1的n+1次多项式,则:
![]()
4.2.2 余项及误差估计
定理![]() 在区间
在区间![]() 上有直到n+1阶的导数,
上有直到n+1阶的导数,![]() 是
是![]() 在n+1个结点
在n+1个结点![]()
![]() 处的n次拉格朗日插值多项式,则对任何
处的n次拉格朗日插值多项式,则对任何![]() 有余项公式:
有余项公式:![]() 。 (4.2.7)
。 (4.2.7)
其中![]() ,
,![]() 且依赖于
且依赖于![]() 。若
。若![]() ,则有误差估计:
,则有误差估计:![]() ≤
≤![]() 。
(
。
(
由存在性唯一性定理可知,拉格朗日插值多项式![]() 与一般多项式
与一般多项式![]() 相同,因此拉格朗日插值多项式所确定的余项公式与定理
相同,因此拉格朗日插值多项式所确定的余项公式与定理
⑴ 若![]() 本身就是次数不超过
本身就是次数不超过![]() 次的多项式,则有:
次的多项式,则有:![]() 。
。
⑵ 在误差估计公式![]() ≤
≤![]() 中,当插值点
中,当插值点![]() 在某结点的邻域内时,误差可能会很小。而在一般情况下,不能保证误差会很小,这将取决于
在某结点的邻域内时,误差可能会很小。而在一般情况下,不能保证误差会很小,这将取决于![]() 以及
以及![]() 的值,如果
的值,如果![]() 和
和![]() 的值较大时,误差可能会较大,说明当
的值较大时,误差可能会较大,说明当![]() 时,误差不一定趋向于零,即插值多项式随次数的增加不一定收敛于被插值函数。
时,误差不一定趋向于零,即插值多项式随次数的增加不一定收敛于被插值函数。
⑶ 余项公式(4.2.)与泰勒公式余项![]() 是不同的,前者涉及到
是不同的,前者涉及到![]() 个结点的乘积
个结点的乘积![]() ,而后者仅涉及一个点的
,而后者仅涉及一个点的![]() 次幂。
次幂。
对线性插值有以下的结论:![]()
且当![]() 时,
时,![]() 。
(
。
(
但对大多数函数而言,插值余项会随插值结点的增加而减小,因而可以用增加插值结点的方法来提高插值公式的精度。
定理 ![]() ,则当
,则当![]() ,
,![]() 时(等距插值),有:⑴
线性插值的误差估计为:
时(等距插值),有:⑴
线性插值的误差估计为:![]()
⑵ 二次插值多项式的误差估计为:![]()
⑶ 三次插值多项式的误差估计为:![]()
*4.2.3
MATLAB程序
% Lagrange插值公式
function dk=ldk421(x,fx,inx)
n=length(x);
m=length(inx);
for i=1:m;
z=inx(i);
s=0.0;
for
k=1:n;
p=1.0;
for
j=1:n;
if
j~=k
p=p*(z-x(j))/(x(k)-x(j));
end
end
s=p*fx(k)+s;
end
f(i)=s
end
*4.2.4
理论证明
定理![]() ,
,![]() …,
…,![]() 为n+1个互异的结点,
为n+1个互异的结点,![]() 为拉格朗日n次基本插值多项式,则有以下结论:⑴
为拉格朗日n次基本插值多项式,则有以下结论:⑴ ![]()
⑵ ![]()
⑶ 设![]() 为任意一个首1的n+1次多项式,则:
为任意一个首1的n+1次多项式,则:
![]()
定理 ![]() ,则当
,则当![]() ,
,![]() 时(等距插值),有:⑴
线性插值的误差估计为:
时(等距插值),有:⑴
线性插值的误差估计为:![]()
⑵ 二次插值多项式的误差估计为:![]()
⑶ 三次插值多项式的误差估计为:![]()