§4.4
Hermite插值方法
前面介绍的代数插值多项式，包括分段低次插值多项式，只要求插值多项式在各结点处满足插值条件，因而无法保证插值多项式及分段插值多项式在结点处导数的连续性，所以，插值函数曲线的光滑度可能很差，这种插值多项式往往还不能全面反映被插值函数的性态，为了得到具有一定光滑程度的函数，许多实际问题不但要求插值函数与被插值函数在各结点处的函数值相同，而且还要求插值函数在某些结点或全部结点上与被插值函数的导数值也相等，甚至要求高阶导数值也相等，这样的插值函数一定能更好地逼近被插值函数，我们称满足这种要求的插值问题为埃尔米特插值问题。
定义
在n＋l个互异的点处的函数值和直到
阶的导数值，若存在函数
满足条件：
，
，其中
，
。则称为函数在n＋l个结点上的埃尔米特插值函数。若是代数多项式，则称为埃尔米特插值多项式。
一般地，如果要求插值函数具有m阶光滑度，可以给出函数在结点上的1至m阶导数值。我们不去讨论上述一般的埃尔米特插值问题，而只是讨论几种最简单，但也是最常用的情形。
为了得到具有一阶光滑度的函数，在结点上除给出函数值外，还要给出一阶导数值，即要求插值多项式满足条件：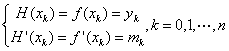
。
显然，满足上述条件的Hermite插值是最简单的情形。因为要满足2n＋2个条件，因此是一个次数不超过2n＋l的多项式。比如，当n＝2时，三个结点的插值多项式将是一个5次多项式。由于高次插值多项式的收敛性和稳定性都不能得以保证，因此可以采取分段插值法。
4.4.1 两点三次的Hermite插值
已知函数在结点
上的函数值以及一阶导数值，求一个三次Hermite插值多项式
使其满足：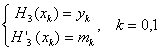
。 (
设
，
，
，
都是三次多项式，并且满足以下条件：
，
(
，
(
将它们的线性组合记为：
，
其中
为待定参数。则称，，，为Hermite插值基函数。当
，
时，插值基函数的图形如下：
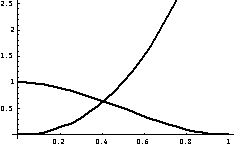
令满足插值条件(，和，的性质，立即可以得到：
＝
，
，
，于是：
(
由基函数所满足的条件可以求出这些基函数。
首先来求。从条件(
，所以结点
是的二重零点，即应含有因式
，并且是不超过三次的多项式，故可设：
，其中
和
为待定参数。再由
及
，解出待定参数和：
，
，
代入整理后得：
同理：
,
将，，，表达式代入(
(