§4.4
分段低次插值方法
4.4.1 高次插值多项式的问题
本节提出这样一个问题:在指定的插值区间上,用![]() 的插值多项式
的插值多项式![]() 近似代替
近似代替![]() ,其误差是否会随插值结点的加密(多项式的次数增高)而减小?回答是对于某些函数,适当地提高插值多项式的次数,会提高计算精度。当函数是连续函数时,增加插值结点虽然使插值函数与被插值函数在更多结点上的取值相等,但由于插值多项式函数在某些非结点处的振荡可能加大,因而可能使在非结点处的误差变得很大。另外,结点的增加会提高插值多项式的计算次数,也不利于控制舍入误差。
,其误差是否会随插值结点的加密(多项式的次数增高)而减小?回答是对于某些函数,适当地提高插值多项式的次数,会提高计算精度。当函数是连续函数时,增加插值结点虽然使插值函数与被插值函数在更多结点上的取值相等,但由于插值多项式函数在某些非结点处的振荡可能加大,因而可能使在非结点处的误差变得很大。另外,结点的增加会提高插值多项式的计算次数,也不利于控制舍入误差。
二十世纪初,Runge对于函数![]() ,
,![]() ,取等距的插值结点:
,取等距的插值结点:![]() ,
,![]() ,
,![]() 。做Lagrange插值多项式:
。做Lagrange插值多项式:
![]()
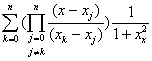 (
(
在接近区间两端点附近,![]() 与
与![]() 的偏离很大,次数越高偏离越大。比如
的偏离很大,次数越高偏离越大。比如![]() =1.80438,而
=1.80438,而![]() =0.4160。Runge还进一步证明了,在结点等距的条件下,当
=0.4160。Runge还进一步证明了,在结点等距的条件下,当![]() 时,由式(
时,由式(![]() 只在
只在![]() 内收敛,除此范围以外,有:
内收敛,除此范围以外,有:
![]()
后来就把插值多项式不收敛的现象称作Runge现象。下图分别给出了当![]() 时的图形。
时的图形。
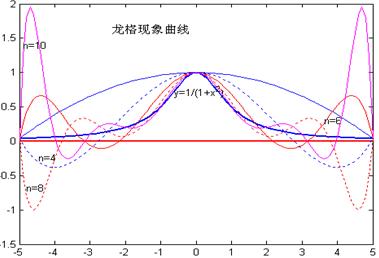
Runge现象说明并非插值多项式的次数愈高,其精度就愈高。
4.4.2 分段低次插值法
设给定![]() 在结点处的函数值,欲求插值多项式。当n较大时,为克服高次插值多项式的弊端,将区间[
在结点处的函数值,欲求插值多项式。当n较大时,为克服高次插值多项式的弊端,将区间[![]() ,
,![]() ]划分为若干个插值子区间,子区间的分法与子区间上插值多项式的次数,以及插值点的位置有关,区间分点应取在结点上,在每一个子区间上做低次插值多项式。这样,所有插值子区间上的插值多项式将构成区间[
]划分为若干个插值子区间,子区间的分法与子区间上插值多项式的次数,以及插值点的位置有关,区间分点应取在结点上,在每一个子区间上做低次插值多项式。这样,所有插值子区间上的插值多项式将构成区间[![]() ,
,![]() ]上的分段函数,称之为
]上的分段函数,称之为![]() 的分段插值多项式。
的分段插值多项式。
1 分段线性插值
设函数![]() 有
有![]() 个插值结点
个插值结点![]() ,取每相邻的两个结点形成一个插值子区间
,取每相邻的两个结点形成一个插值子区间![]() ,在插值子区间中做线性插值多项式:
,在插值子区间中做线性插值多项式:
![]() ,
,![]() 。 (
。 (
令: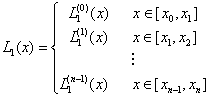 ,则有
,则有![]() ,
,![]() 。
。
故称![]() 为
为![]() 在区间[
在区间[![]() ,
,![]() ]上的分段线性插值多项式。
]上的分段线性插值多项式。
分段线性插值多项式的图形是连接平面上的点的一条折线。因此,在结点处曲线往往出现尖拐点,所以分段线性插值函数的光滑性不好。
【例![]() 在点
在点![]() 6.5,7.2处的近似值。
6.5,7.2处的近似值。
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
12 |
234 |
34 |
-1 |
34 |
2 |
5 |
23 |
34 |
9 |
45 |
23 |
x=[1:12];fx=[12 234 34 -1 34 2 5 23 34 9 45 23];
xk=[1:0.2:12];y=interp1(x,fx,xk);plot(x,fx,xk,y)
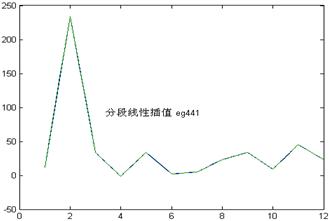
由余项公式可知,![]() 的余项为:
的余项为:![]()
![]() ,
,![]() 且
且![]() 依赖于
依赖于![]() 。 (
。 (
![]() (
(
其中![]() ,
,![]() ,
,![]() 。
。
2 分段二次Lagrange插值
当给定的函数表中结点的个数远多于3的时候,为了提高计算精度,或根据实际问题需要,有时采取分段二次插值法。对于给定的插值点![]() ,应取靠近
,应取靠近![]() 的三个结点做二次插值多项式。分段二次插值的计算公式为:
的三个结点做二次插值多项式。分段二次插值的计算公式为:
![]()
![]()
![]() ,
,![]() (
(
【例![]() 在点
在点![]() 6.5,7.2处的近似值。
6.5,7.2处的近似值。
解 因为![]() 6.5
6.5![]() ,可以取
,可以取![]() =6,
=6,![]() =7,
=7,![]() =8为结点,而
=8为结点,而![]() 7.2
7.2
![]() 但靠近6,所以仍然取上面的三个结点,于是,计算
但靠近6,所以仍然取上面的三个结点,于是,计算![]() 与
与![]() 的分段二次插值公式一样,将结点值及相应的函数值代入公式(
的分段二次插值公式一样,将结点值及相应的函数值代入公式(
![]()
![]()
![]()
计算后有如下结果:![]() ≈1.6250,
≈1.6250,![]() ≈7.4000。
≈7.4000。
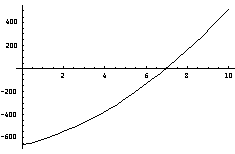
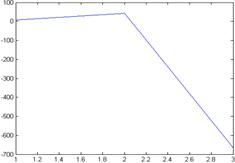
上面计算的各插值点的函数值是符合函数表中函数值变化规律的。