5.1 数值积分概述

5.1.1 数值积分的基本思想

计算定积分的困难关键在于被积函数的复杂性。为此将用简单函数近似代替是构造数值积分算法的基本思想。

由定积分的定义＝可知，定积分是一个“和式极限”，该极限的几何意义就是由＝，直线＝，＝以及轴所围曲边梯形的面积。由积分中值定理可知：

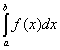＝(b－a)， ()

其几何意义是：上述曲边梯形的面积等于一个矩形的面积。换个角度来考虑此问题，若用直线段，其中，近似代替曲线段，，则可得矩形积分公式：

＝(b－)， () 　　(5.1.1)

特别地，当＝，＝，＝b时分别称之为左矩公式、中矩公式及右矩公式。

若以过点A(，)，B(b，(b))的直线段：y＝＋(－)近似代替曲线段y＝f(x)，则得梯形公式：

≈T＝[＋] 　 (5.1.2)

若考虑过点A(，)，C(，())，B(b，(b))的抛物线段：

y＝px²＋qx＋r，(a≤x≤b)，其中p，q，r由以下方程组

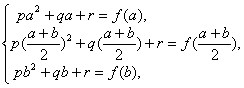
确定，用该抛物线段近似代替曲线段，则可得Simpson公式：

≈S＝[＋4()＋] (5.1.3)

前面几个公式实际上是在定积分的定义中，不取极限而用有限个结点x_k处的函数值f(x_k)进行适当加权求和而得到的和式近似公式。这类公式的一般形式为：

≈， (5.1.4)

数值积分就是将定积分的计算用和式近似表示，上式中的x_k称为求积结点，A_k称为求积系数。这是用被积函数f(x)在节点x_k的函数值f(x_k)的某种线性组合来近似计算定积分，称之为机械求积公式。鉴于其系数A_k仅与结点的选择有关而与被积函数f(x)无关的常数，因此求积公式(5.1.4)具有通用性。公式(5.1.4)中的和式称为求积算式，而余项R[f]＝－ (5.1.5)

称为求积公式的截断误差。确定求积公式(5.1.4)，也就是确定其中的求积结点x_k和求积系数A_k。

数值积分的特点是直接用积分区间[a，b]上的一些离散结点上的函数值f(x)的线性组合计算定积分的近似值，从而将定积分的计算归结为函数值的计算，这就避开了Newton——Leibniz公式中需要寻求原函数的困难，并为用计算机求积分提供了可行性。但要注意的是，不应该把求积公式(5.1.4)看作是针对某一特定的函数f(x)，而应该把它看作是区间[a，b]上函数整体来讲，所以求积公式也常用：

I[f]＝Q[f]＋R[f] (5.1.6)

来表示。

5.1.2 代数精度法

数值求积方法是近似方法，为了研究其精度，常用代数精度这个概念来说明。由Taylor展开定理可知，任一充分可微函数f(x)均能展开为一个关于x的多项式与其余项的和。因此，若要求定积分的近似计算具有一定的精度，则需公式(5.1.6)对零次到足够大的正整数n次的多项式能准确成立，为此引入代数精度的定义。

定义 若求积公式(5.1.6)对所有次数不超过n的代数多项式P(x_n)都精确成立，即R[P_n(x)]≡0，而对于某个n＋l次多项式P(x_n＋1)不能精确成立，即R[P_n+1(x)]≠0，则称此求积公式具有m次代数精度。

求积公式的代数精度概念是衡量公式逼近好坏的标准之一。

一般而言，从上述定义来直接判断求积公式的代数精度比较困难．而由多项式和定积分的性质，容易证明上述定义等价于：若依次用＝1，x，x²，…，代入求积公式(5.1.6)，均有：，(m＝0，1,…,n)，而用＝代入求积公式(5.1.6)，有。显然，代数精度越高，求积公式的近似程度越好。

可以直接验证矩形公式具有0次代数精度，梯形公式具有1次代数精度，而Simpson公式具有3次代数精度。

以代数精度作为标准可获得构造求积公式的一种方法，称之为代数精度法。如果令公式(5.1.6)对f(x)＝1，x，x²，…，xⁿ准确成立，那么可线性方程组：

＝＝ (m＝0，1,…,n)

当结点(＝0，1，…，n)给定且互异时，求积系数可由上式确定。

例5.1.1 试确定一个具有3次代数精度的公式：

≈

解 要具有3次代数精度，必需满足以下方程：

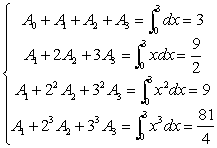
解之得：

由此即得公式：≈［(0)＋3(1)＋3(2)＋(3)］

且将＝x⁴代入上式时，不能精确成立(有误差)，故所得公式具有3次代数精度。

例5.1.2 设有求积公式：≈A₀(－1)＋A₁(0)＋A₂(1)

试确定系数A₀，A₁，A₂，使上述求积公式的代数精度尽量高，并指出该求积公式所具有的代数精度。

解 令求积公式依次对＝1，x，x²都精确成立，即系数A₀，A₁，A₂，应满足方程组：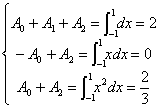

解得：A₀＝，A₁＝，A₂＝，因此，该求积公式应为：

≈(－1)＋(0)＋(1)

又容易验证，该求积公式对于＝x³也精确成立，但对＝x⁴，求积公式不能精确成立。因此，该求积公式具有三次代数精度。

凡至少具有零次代数精度的求积公式(5.1.6)，一定满足：＝，

从而有：＝，即求积系数A_k之和等于积分区间的长度，这是求积系数的基本特征。

5.1.3 插值求积法

从数值逼近的观点看，对定积分只要能找到一个逼近被积函数足够好，又易于求积分的简单函数P(x)近似代替f(x)从而就有：≈

因此，构造数值求积公式的方法很多，常用的一个方法是利用插值多项式来构造。具体做法是，对于定积分＝，如果已知被积函数在积分区间[a，b]上的一组结点a≤x₀<x₁<…<x_n≤b上的函数值(x₀)，(x₁)，…，(x_n)，则可构造出(x)的n次拉格朗日插值多项式：L_n(x)＝，其中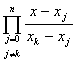＝，由于代数多项式的原函数容易求出，则有：

≈＝＝

这样就得到了一个数值求积公式：≈，其中：

，

我们称求积系数由上式确定的求积公式为插值型求积公式。利用插值余项可得插值型求积公式的余项是：R[f]＝I[f]－Q[f]＝ (5.1.7)

对于插值型求积公式，当被积函数f(x)取次数不超过n次多项式时，由于，所以余项R[f]＝0，即求积公式对一切次数不超过n的多项式精确成立，所以含有n＋l个结点x_k(k＝0，1，…，n)的插值型求积公式至少具有n次代数精度。反之，也容易证明，如果一个求积公式的代数精度至少是n次，那么它可看成是利用插值多项式推导出来的。