§5.2
牛顿——柯特斯求积公式
为了使求积公式的形式简单,下面讨论等距结点下的插值型求积公式。将积分区间![]() 分成n等分,令h=
分成n等分,令h=![]() ,称之为步长,求积结点
,称之为步长,求积结点![]() 为等距结点,
为等距结点,![]() ,(
,(![]() =0,l,…,n),且对应的函数值
=0,l,…,n),且对应的函数值![]() (
(![]() )为已知,则以这些等距结点为插值结点所导出的插值型求积公式就称为牛顿——柯特斯求积公式,简记为N-C公式。下面介绍几个常用的低阶牛顿——柯特斯求积公式。
)为已知,则以这些等距结点为插值结点所导出的插值型求积公式就称为牛顿——柯特斯求积公式,简记为N-C公式。下面介绍几个常用的低阶牛顿——柯特斯求积公式。
5.2.1 低阶牛顿-柯特斯求积公式
首先考察n=1时的情形,![]() =
=![]() ,
,![]() ,以区间
,以区间![]() 的两个端点
的两个端点![]() ,
,![]() 为结点,构造一次插值多项式:
为结点,构造一次插值多项式:
![]() =
=![]() =
=![]() ×
×![]() +
+![]() ×
×![]() ,则:
,则:
![]()
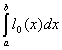 =
=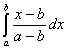 =
=![]()
![]()
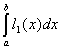 =
=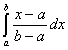 =
=![]()
因此可得:![]() ≈
≈![]() =
=![]() [
[![]() +
+![]() ]=T
]=T
这就是前面的梯形公式(
其次我们考察n=2时的情形,这时有三个结点,除两个端点![]() ,
,![]() 外,再增加中点
外,再增加中点![]() ,以x0=
,以x0=![]() ,x1=c,x2=b为结点,构造二次插值多项式:
,x1=c,x2=b为结点,构造二次插值多项式:
![]()
=![]() +
+![]() +
+![]()
则:![]()
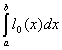 =
=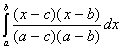 =
=![]()
![]()
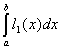 =
=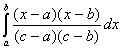 =
=![]()
![]()
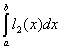 =
=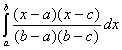 =
=![]()
因此可得:![]() ≈
≈![]()
=![]() [
[![]() +
+![]() +
+![]() ]=S
]=S
容易看出这就是前面的辛普森(Simpson)公式(![]() 下的面积近似代替曲线
下的面积近似代替曲线![]()
![]() 下的面积。
下的面积。
例![]() 和指数函数
和指数函数![]() 在区间[-2,0]上积分。计算结果如下表所示。表中结果说明辛普森公式相对梯形公式而言,较为准确一些,因此其使用价值也相对较大。
在区间[-2,0]上积分。计算结果如下表所示。表中结果说明辛普森公式相对梯形公式而言,较为准确一些,因此其使用价值也相对较大。
|
函数 |
|
|
|
|
|
|
|
精确值 |
2 |
-2 |
2.667 |
-4 |
6.4 |
0.865 |
|
梯形值 |
2 |
-2 |
4 |
-8 |
16 |
1.135 |
|
辛普森值 |
2 |
-2 |
2.667 |
-4 |
6.667 |
0.869 |
最后考虑n=4的情形,这时共有5个结点。![]() =
=![]() ,(k=0,1,2,3,4),类似前面的方法,可以推出下列柯特斯公式:
,(k=0,1,2,3,4),类似前面的方法,可以推出下列柯特斯公式:
![]() ≈
≈![]()
=C=![]() [7
[7![]() +
+![]() +
+![]() +
+![]() +
+![]() (
(
由插值型求积公式:![]() ≈
≈![]() ,其中
,其中
![]()
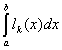 =
=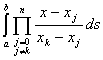 ,(k=0,1,2,…,n),
,(k=0,1,2,…,n),
可得一般的牛顿——柯特斯公式。为计算简便,作变换x=a+sh,则:dx=hds,xk-xj=(k-j)h,x-xj=(s-j)h,(j=0,l,2,…,n)
从而:lk(x)=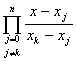 =
=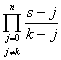 , (k=0,1,2,…,n)
, (k=0,1,2,…,n)
则:![]()
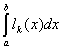 =h
=h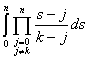 =h
=h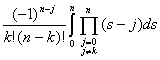 ,
,
如果再令![]()
![]()
![]() ,则称
,则称![]() 为柯特斯系数,由此可得一般的牛顿——柯特斯求积公式:
为柯特斯系数,由此可得一般的牛顿——柯特斯求积公式:![]() ≈
≈![]()
![]() (
(
在牛顿——柯特斯求积公式中,最重要的是:n=1,2,4三个公式,即梯形公式、辛普森公式和柯特斯公式。
不难证明,柯特斯系数![]() 具有对称性,即:
具有对称性,即:![]() =
=![]() ,(k=0,1,…,n)
,(k=0,1,…,n)
因此,在下面的柯特斯系数表中,后几行只列出了一部分。同时,柯特斯系数![]() 还满足:
还满足:![]() =1。这个等式可以检验求积系数的计算是否正确。
=1。这个等式可以检验求积系数的计算是否正确。
柯 特 斯 系 数 表
|
N |
C |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
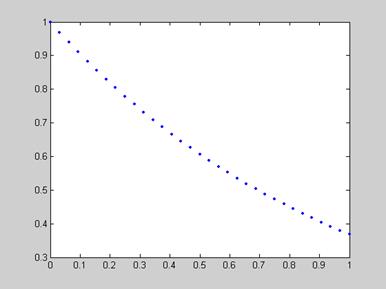
利用8阶牛顿——柯特斯公式计算积分:![]()
在MATLAB中,直接调用quad、quadl或quad8。调用格式为:
quad(f,a,b,eps,trace),其中f为被积函数,a,b分别是积分上下限,eps为绝对误差限,trace为输入参数,非零值则作出积分图,否则不作图。
>> quad8('funout',0,1,0.00001)
ans =
0.6321
>> quad8('funout',0,1,0.00001,1)
ans =
0.6321
>> quad('funout',0,1,0.00001)
ans =
0.6321
>> quad('funout',0,1,0.00001,1)
9 0.0000000000 2.71580000e-001 0.2378256930
11 0.2715800000 4.56840000e-001 0.2795033003
13 0.7284200000 2.71580000e-001 0.1147915670
ans =
0.6321
>> quad('funout',0,1,0.00001,1)
9 0.0000000000 2.71580000e-001 0.2378256930
11 0.2715800000 4.56840000e-001 0.2795033003
13 0.7284200000 2.71580000e-001 0.1147915670
ans =
0.6321
>> quad8('funout',0,1,0.00001,1)
ans =
0.6321
>> quadl('funout',0,1,0.00001,1)
18 0.0000000000 5.00000000e-001 0.6321205588
ans =
0.6321
* 5.2.3 理论证明
下面分别推导梯形公式、辛普森公式、柯特斯公式和一般的牛顿——柯特斯插值型求积公式的余项表达式,并讨论牛顿——柯特斯插值型求积公式的稳定性问题。
在推导插值求积公式的余项时,需要用到定积分中值定理,即:
如果函数f(x)、g(x)ÎC[a,b],且g(x)在(a,b)区间上不变号,则存在![]() (a,b),使等式:
(a,b),使等式: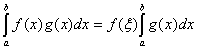 成立。
成立。
1
梯形公式的余项R(T)
由余项公式(![]() =
=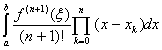 ,可得:
,可得:
R(T)
=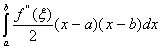 ,
, ![]() (a,b)
(a,b)
因为![]() 在区间(a,b)上恒为负,因此根据定积分中值定理,有:R(T) =
在区间(a,b)上恒为负,因此根据定积分中值定理,有:R(T) =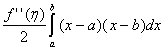 =-
=-![]() ,
,![]() (a,b) (
(a,b) (
2 辛普森公式的余项R(S)
同样由余项公式(![]() =
=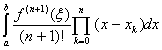 ,可得:
,可得:
R(S)=![]()
但因为函数![]() 在区间(a,b)上变号,因而不能直接应用定积分中值定理导出R(S)的表达式。为了得到R(S)的表达式,常用的方法是作f(x)的Hermite插值多项式H(x),因而有:
在区间(a,b)上变号,因而不能直接应用定积分中值定理导出R(S)的表达式。为了得到R(S)的表达式,常用的方法是作f(x)的Hermite插值多项式H(x),因而有:
![]() =
=![]()
同时因为辛普森公式具有3次代数精度,从而可推得:
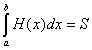 =
=![]()
因此:R(S)=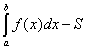 =
=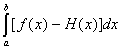
=![]()
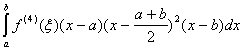
=-![]() =-
=-![]()
=-![]() ,
,![]() (a,b)
(
(a,b)
(
3
柯特斯公式的余项R(C)
关于柯特斯公式的余项R(C),有如下结果:
R(C)=-![]()
=-![]() ,
,![]() (a,b)
(
(a,b)
(
通过余项公式可以看出,梯形公式只有一次代数精度,而抛物线求积公式却有三次代数精度,柯特斯公式具有五次代数精度。事实上,利用余项公式(![]() 的余项也为零,从而求积公式依然精确成立,所以有以下结论:
的余项也为零,从而求积公式依然精确成立,所以有以下结论:
定理 对于n阶的牛顿——柯特斯求积公式:
![]() ≈
≈![]()
![]()
当n为奇数时,至少具有n次代数精度;当n为偶数时,至少具有n+1次代数精度。
4
牛顿——柯特斯公式的稳定性与收敛性
数值计算的稳定性问题是指初始数据的误差和计算过程中的误差对计算结果的影响大小问题。在数值积分中,由于计算各结点上的函数值![]() 时可能产生误差,使实际得到的数值
时可能产生误差,使实际得到的数值![]() 有误差¶k=f(xk)-f*(xk),若记和式I*n=
有误差¶k=f(xk)-f*(xk),若记和式I*n=![]() ,In=
,In=![]() ,如果其数值积分的计算误差小于给定的正数¶,即∣f(xk)-f*(xk)∣≤¶,则称求积公式的计算是稳定的。
,如果其数值积分的计算误差小于给定的正数¶,即∣f(xk)-f*(xk)∣≤¶,则称求积公式的计算是稳定的。
由于柯特斯系数Ck及结点值xk都能相当精确地给出,因而,使用牛顿——柯特斯插值型求积公式计算积分时,舍入误差的影响主要来自于函数值![]() 的计算。
的计算。
设![]() 为准确值,
为准确值,![]() 为计算值,误差¶k=f(xk)-f*(xk),因而利用公式(
为计算值,误差¶k=f(xk)-f*(xk),因而利用公式(![]()
![]() ,
,
它与理论值In=![]()
![]() 的误差为:
的误差为:
In-I*n=![]()
![]() =
=![]()
![]()
记¶=![]() ,如果所有的求积系数Ck均为正数,则得:
,如果所有的求积系数Ck均为正数,则得:
![]() =
=![]() ≤¶
≤¶![]()
![]() =¶
=¶![]()
即当所有的Ck全为正数时,如果各结点处函数值f(xk)的绝对误差限均不超过¶,则结果的误差积累不超过¶![]() ,因而方法是稳定的。但若Ck有正有负(例如n≥8),将有:¶
,因而方法是稳定的。但若Ck有正有负(例如n≥8),将有:¶![]()
![]() >¶
>¶![]() ,因而方法的稳定性无法保证。可以证明:当n变大时,
,因而方法的稳定性无法保证。可以证明:当n变大时,![]() 是无界的,这种情况增大了舍入误差的影响,求积公式不宜使用。
是无界的,这种情况增大了舍入误差的影响,求积公式不宜使用。
在求积公式(.1.4)中,若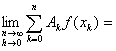
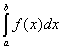 ,其中h=
,其中h=![]() ,则称求积公式
,则称求积公式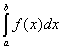 ≈
≈![]() 是收敛的。可以证明,并非任何连续函数f(x),当
是收敛的。可以证明,并非任何连续函数f(x),当![]() 时都有
时都有![]() ,即牛顿——柯特斯求积公式的收敛性也没有保证。因此,在实际计算时,很少使用高阶的牛顿——柯特斯插值型求积公式。
,即牛顿——柯特斯求积公式的收敛性也没有保证。因此,在实际计算时,很少使用高阶的牛顿——柯特斯插值型求积公式。