§5.3
复合求积公式
由于在实际计算时，不宜使用高阶的牛顿——柯特斯公式，但若积分区间较大，单独用一个低阶的牛顿——柯特斯公式来计算积分的近似值，显然精度不好，为了提高数值求积的精确度，可利用积分对区间的可加性来解决这个问题，这就是通常采用的复合求积法。所谓复合求积法，其指导思想就是先将积分区间分成若干个小区间，在每个小区间上采用低阶求积公式进行计算，然后把所有子区间的计算结果相加得出新的求积公式，这种公式就叫做复合求积公式。
5.3.1 低阶复合求积公式
1 复合梯形求积公式
如果在区间(a，b)上直接应用梯形公式则可得(
)：
T1＝
＝
若在区间(
，b)中，增加一个结点
，则把区间(，b)分成两个小区间(，c)与(c，b)，在两个小区间上分别应用梯形公式，然后相加就会得出新的求积公式T2：(其中
)
T2＝
＋
＝
继续增加结点，把区间(，b)分成4等分，(，x1) 、(x1，x2)、 (x2，x3) 、(x3，b) ，在每个小区间上分别应用梯形公式后再相加，就会得出新的求积公式
：
T4＝
＋
＋
＋
(其中
)，
＝
其中
＝
，（
＝0，l，…，4）
同理，把区间(a，b)分成8等分时，可得求积公式T8：
T8＝
上面我们将区间(，b)分成
等分，是为了在计算后面的数值时，充分利用到前面的数据。在一般情况下，若把区间(，b)分成n等分，记结点为xk＝＋kh，（k＝0，l，…，n），h＝(b－)/n，在每一个小区间[xk，xk－1]上应用梯形公式，则有：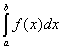
＝
≈
＝
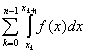就可导出复合梯形公式Tn＝
(
利用梯形公式的余项公式(
R(Tn)＝－
＝－
， 
(a，b)
(
例
。
解 该积分的精确值是
≈3.141592654。此时＝0，b＝1，下面分别用T1、T2、T4、T8进行计算。函数f(x)＝4/(1＋x2)在各结点上的值可列表如下：
|
xk |
0 |
1/8 |
2/8 |
3/8 |
4/8 |
|
f(xk) |
4.0000 |
3.93846 |
3.76470 |
3.50685 |
3.20000 |
|
xk |
5/8 |
6/8 |
7/8 |
1 |
|
|
f(xk) |
2.87640 |
2.56000 |
2.26549 |
2.00000 |
|
T1＝
＝3
T2＝1/4×
＝3.1000
T4＝1/8×
＝3.13117
T8＝1/16×
＝3.13198
T8与准确值之间的误差为：－T8≈0.26×
<0.5×
，即T8只有三位有效数字。
如果要求误差不超过
，就必须对函数f(x)＝4/(1＋x2)的二阶导数在区间[0，1]上的最大值作出估计。因为：
，
，
>0
可见
在区间[0，1]上是单调增函数，(0)＝－8，(1)＝0，因此，M＝
＝8，则Tn的截断误差为：R(Tn)＝
＝
若要求
≤，即
，则
817。
由这个例题可以看出，梯形公式的精确度比较低，收敛也比较慢，因此，梯形公式并不直接用来计算积分，而是为其它的积分法(如龙贝格积分法)提供初始数据，在那里，由梯形公式得出的这些不够准确的近似值，将被一些简单的运算加工后变得非常准确。
2 复合辛普森求积公式
在区间(，b)上直接应用辛普森公式，需要三个结点
，其中
，就可得出求积公式S1：(其中
)
S1＝
＝
若在区间(，b)中，增加一些结点<x1<c<x2<b，把区间(，b)分成两个小区间(，c)与(c，b)，在两个小区间上分别应用辛普森公式，然后相加就会得出新的求积公式S2：(其中
)
S2＝
＋
同理，继续增加一些结点，把区间(，b)分成4等分，分别在每个小区间上应用辛普森公式，再相加就可得求积公式S4：(其中
)
S4＝
＝
＋
其中＝，（＝0，l，…，8）
一般情况下，由于辛普森公式需要三个结点，因此在区间(，b)内插入2n－1个结点：＝x0<x1<x2<…<x2n－1<x2n＝b，将区间(，b) 2n等分，其中＝
其中＝0，l，…，2n，hn＝
，这样就可以把区间(，b)分成下列n个小区间：［x0，x2］，［x2，x4］，…，［x2n－2，x2n］，在每个小区间上使用辛普森公式可得：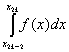
≈
＝
将各子区间上的求积公式相加，就得到复合辛普森公式Sn：
Sn＝
＋
其截断误差为：R(Sn)＝－
， (，b)
3
复合柯特斯求积公式
同理可得下面的复合柯特斯公式：
C1＝
[7
＋
＋
＋
＋
]
C2＝
｛7＋
＋
＋｝
其中＝
，（＝0，l，…，8）
Cn＝
｛7＋
＋
＋
＋｝
其中＝
，（＝0，l，…，4n）
其截断误差为：R(Cn)＝－
，
例7.3.2 使用复合辛普森公式S1、S2、S4及复合柯特斯公式C2重新计算例
解
S1＝1/6×
＝3.133333
S2＝1/12×
＝3.14156
S4＝1/24×
＝3.14159
C1＝1/90×
＝3.14211
C2＝1/180×
＝3.14159
计算T8、S4、C2时，都需要区间上的9个结点处的函数值的线性组合，只是组合方式不同，计算量相差甚微，但S4、C2的精度很高，而T8的精度较低，这项计算表明，复合辛普森公式的计算复杂性居中，精度又高，是一个较好的数值积分法，因此使用比较广泛。
同时容易证明，以上三个复合求积公式(梯形公式、辛普森公式、柯特斯公式)，当步长h→0时均收敛，而且收敛速度一个比一个快，并且它们的计算也都是数值稳定。
5.3.2 区间逐次分半求积法
上面介绍的几种复合求积法对提高积分的精度是行之有效的，但在使用求积公式前，必须给出适当的步长。当被积函数
在区间[，b]上的高阶导数容易估计时，利用截断误差公式可以预先确定计算的精度
，并可以估计出用复合梯形法或复合抛物线法时的步长h。但在很多情况下，被积函数导数的界很难估计，这就使得直接预先确定步长h有很大的困难。下面介绍一种在计算过程中能自动选取步长的“变步长求积法”，也称为区间逐次分半法。其基本思想是：在步长逐次折半过程中，反复用复合求积公式计算，直到二分前后的两次积分计算结果之差的绝对值
小于允许的精度为止，并取
作为所求的积分近似值，这样计算时，步长h不是固定不变的，因此叫做变步长求积法。
以复合梯形求积法为例，由复合梯形公式的截断误差公式可知：
R(Tn)＝
＝－
R(T2n)＝
＝－
变步长算法
前面介绍的复化梯形公式，复化Simpson公式，复化htes公式对提高精度是非常有效的，在利用上述公式时，步长都是固定的，因此称为定步长的复化求积公式。在使用上述方法之前，需要首先确定一个合适的步长，但是步长取得太大，精度难以保证，而如果步长取得太小，则会加大计算量。而事先给出一个合适的步长往往存在很大困难。由此，实际上一般常采用变步长的求积方法，即让步长逐次折半（步长二分）的过程中，反复使用复化求积公式计算，直到相邻两次计算结果之差的绝对值小于允许的精度要求时停止计算，这种方法称为变步长的算法。下面重点就变步长的梯形公式进行分析。对于积分：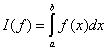
，将区间[，b] n等分，共有n＋1个分点
＝＋
，k＝0，1，…，n。步长h
，按复合梯形公式(
Tn＝
计算，共需计算n＋1次函数值。现将步长折半，再将每个子区间[，
]二分一次，分点增至2n＋1个。设上述子区间的中点为：
，在[，]上用复合梯形公式(
，
从而有：
即：
上式称为变步长的梯形公式。
由变步长的梯形公式可以看出，当计算T2n时，可以利用前面的结果Tn，剩下的仅仅需要求n个新分点处的函数值计算后一项即可。
为了便于编程序，通常将区间[，b]等分数依次取成：
1＝20，2＝21，4＝22，8＝23，…，
并用
＜
。(为预先给定的精度)控制二分次数，当满足此精度要求时，停止计算，输出
。作为所求积分的近似值，否则再二分。
利用上述方法，用MATLAB编写变步长梯形公式计算积分的程序如下：
function ldk534(a,b,eps)
m=1
t0=0;
t2=(f(a)+f(b))/4+f((a+b)/2)
while
abs(t2-t0)>eps
m=m+1
p=t2;
t1=0;
n=2^m;
h=(b-a)/n;
for k=0:(n-1)
t1=t1+h*((f(a+k*h)+f(a+(k+1)*h))/4+f(a+(k+1/2)*h)/2);
end
t2=t1
t0=p;
end
I=t2
例 计算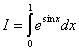
解 首先编写函数程序：
function f=f(x)
f=exp(sin(x));
在Matlab中输入命令：
ldk541(0,1,0.0001)
则输出结果为：m=1 t2=
可以看出，上述计算将积分区间二分了四次，求得 I的近似值为 1.631。