§5.4
龙贝格积分法
在用复化梯形求积公式时,记
为
,其中
.利用定积分定义有
在数值计算中,经常会遇到类似情况:精确值
是所要求的,但不能用有限计算量算出来,而对某些
,
却可以很方便地计算出来.如何从已知的
推出的近似值,为些介绍数值计算中的重要方法;外推方法.
4.1外推原理
定理9 若逼近有下述余项展开
(4.1)
其中
,设
为相近的互异正数,则可用
(4.2)
来近似，其中
满足
（4.3）
而且
.
对于
的情况,我们有：
定理10
若逼近的余项能写成渐近形式
（4.4）
及
是独立于
的常数，则由
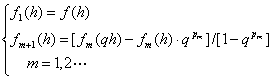（4.5）
定义的序列
随
增大以更快的速度收敛于：
（4.6）
其中
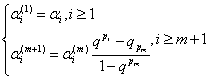（4.7）
定理10也称Richardson外推法。
4．2复化梯形公式余项的渐近展开
利用Euler-Maclaurin求和公式，可以证明复化梯形公式的余项具有渐近展开。
定理11
若
则有
(4.8)
其中
为
数，而
（4.9）
若记
从而可用Richardson外推法提高精度。
4．3
龙贝格算法
在复化梯形公式中，选取
记
注意到
得
（4.10）
计算顺序如表4-7所示。
表4-7
|
|
|
||||||||||||||||||||||||||||
|
0 1 2 3 |
… |
龙贝格算法：
1．输入外推次数
（一般取为3），控制精度
；
2．置
计算
，取
；
3．计算
；
4．对
进行外推计算
；
5．若
，输出数值积分值
，停机；
6．置
，
7．转3。
在龙贝格算法中，第一列对应于复化梯形序列，第二列对应于复化Simpson序列，第三列对应于Cotes序列，第四列称为龙贝格序列。在实际使用中常常只计算到第4段列（即取
），更高的列较少用。龙贝格算法中止准则，一般取同列或同行相邻两高值的的误差绝以值小于事先给定的精度要求。
龙贝格算法是数值稳定的，且对任意连续函数，都能保证数值积分收敛到准确值。龙贝格算法程序简单，当
函数值不太复杂时，龙贝格算法是常用的实用方法。