§5.5 高斯积分公式

前面介绍的n+1个点的 Newton -Cotes求积公式，其特征是节点是等距的。这种特点使得求积公式便于构造，复化求积公式易于形成。但同时也限制了公式的精度。n是偶数时，代数精度为n+1，n是奇数时，代数精度为n 。我们知道 n+1个节点的插值型求积公式的代数精确度不低于n 。设想：能不能在区间[a,b]上适当选择n+1个节点，，，……，，使插值求积公式的代数精度高于n？答案是肯定的，适当选择节点，可使公式的精度最高达到2n+1，这就是本节所要介绍的高斯求积公式。

若存在节点 xi Î[a, b]及求积系数 wi ，使得下面的求积公式具有 2n+1 次代数精度，则称节点 xi 为高斯点，wi 为高斯系数，求积公式为高斯(Gauss)求积公式。

注：(1)Gauss求积公式仍然是插值型求积公式；

(2)Gauss系数可通过Gauss点和Lagrange基函数得到；

回顾插值型求积公式，

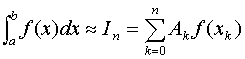
当节点取定时，一般只能保证达到n次代数精度。当节点不限制时，求积公式中有2n+2个待定系数，可以期望有多少次代数精度？可能更高吗？

定义：如果求积公式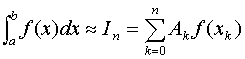具有2n+1次代数精度，则称其为Gauss型求积，并称公式中的节点为Gauss点。

如何选取节点及系数？与被积函数有关吗？只与积分区间及n有关。

例：求积分区间为，时Gauss型求积公式。

对于一般的积分区间，可以通过变量替换（？）转化为上的问题。

对于一般的n值，区间上相应的n+1个Gauss点一定存在，故相应的Gauss型求积公式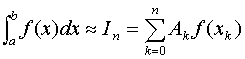一定存在，称为Gauss-Legendre求积公式。