§5.6
数值微分
在微积分中,函数的导数是通过极限定义的.当函数用表格给出时,就只能用数值方法求导数的近似值.
5.6.1 应用泰勒公式估计导数
设已知函数f(x)在结点x0,x1,x2…处的值,根据导数的定义:
![]()
如果以差商![]() /
/![]() 代替
代替![]() 则有:
则有:
![]() ≈
≈![]()
其中![]() 可正可负,取h=
可正可负,取h=![]() ,就有:
,就有:![]() ≈
≈![]() (
(
及 ![]() ≈
≈![]() (
(
公式(![]() 的泰勒公式推得。因为:
的泰勒公式推得。因为:
![]()
![]()
所以有:![]() ≈
≈![]() -
-![]()
![]() ≈
≈![]() +
+![]()
从而可知,前差公式和后差公式的截断误差均为R=O(h)。
若将![]() 和
和![]() 的泰勒展开式多取一项,便有:
的泰勒展开式多取一项,便有:
![]() +
+![]()
![]() -
-![]()
两式相减,解出![]() 可得:
可得:![]() ≈
≈
![]() +
+![]()
舍去余项,就得到一阶导数的中心差分公式:
![]() ≈
≈![]() (
(
公式(
若将![]() 和
和![]() 的泰勒公式再多取一项,然后相加,就可以得到二阶导数的中心差分公式:
的泰勒公式再多取一项,然后相加,就可以得到二阶导数的中心差分公式:![]() ≈
≈![]()
其截断误差也是:R=O(h2)。
5.7.
应用插值公式估计导数
例![]() 的近似值:
的近似值:
|
|
0.00 |
0.90 |
0.99 |
1.00 |
1.01 |
1.10 |
2.00 |
|
|
1.000 |
2.460 |
2.691 |
2.718 |
2.746 |
3.004 |
7.389 |
解 应用中心差分公式(![]() ≈
≈![]()
取不同的步长h=1,0.1,0.01计算,结果见下表.
|
h |
|
误差 |
|
1.0 |
|
0.476 |
|
0.1 |
|
0.002 |
|
0.01 |
|
0.032 |
由计算结果可以看出,当h由1.0减小到0.1时,精度大为提高,但继续减小到0.01时,精度却大幅度下降.在这里看到了计算的不稳定性.因此,在作数值微分时,应特别注意步长的合理选取.
上例的结果还表明,在使用插值多项式估计导数时,当插值多项式![]() 收敛于
收敛于![]() 时,
时,![]() 未必收敛于
未必收敛于![]() ,所以使用高次插值多项式也不一定能提高精度.为此我们可以采用样条函数来估计导数,以提高计算精度.
,所以使用高次插值多项式也不一定能提高精度.为此我们可以采用样条函数来估计导数,以提高计算精度.
回顾导数定义,得
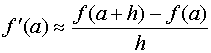
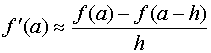

例:用中点公式求![]() 在
在![]() 处的一阶导数(取四位有效数字计算)
处的一阶导数(取四位有效数字计算)
![]()
分别取![]() 进行计算。
进行计算。
对于列表函数![]() (只知道若干个点处函数值),考虑用插值函数的微分来作为近似。即先构造插值函数
(只知道若干个点处函数值),考虑用插值函数的微分来作为近似。即先构造插值函数![]() ,以
,以![]() 的导数近似代替
的导数近似代替![]() 的导数。
的导数。
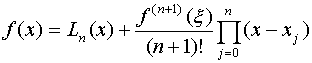 ,
,![]() 与
与![]() 有关。
有关。
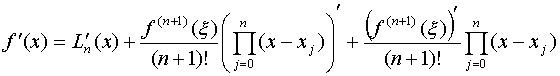
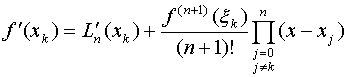
![]() 时,两点公式:
时,两点公式:![]()
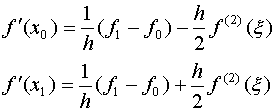
![]() 时,三点公式:
时,三点公式:![]()
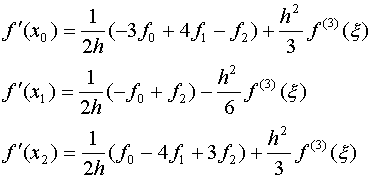
步长![]() 的选择应兼顾截断误差和舍入误差两方面。
的选择应兼顾截断误差和舍入误差两方面。
例:已知![]() ,利用两点公式计算
,利用两点公式计算![]() 的近似值,依次取
的近似值,依次取![]() ,
,![]() 。
。
解:两点公式
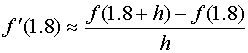
截断误差界为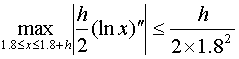
利用三次样条插值多项式求近似导数
练习 5. 1
用复合辛普森公式求积分:![]() 的近似值时,为使截断误差R(Sn)≤0.5×10-4,问需要取多少个结点?
的近似值时,为使截断误差R(Sn)≤0.5×10-4,问需要取多少个结点?
解 复合辛普森公式的截断误差为:R(Sn)=-![]()
所以:∣R(Sn)∣=![]() ≤
≤![]() ≤
≤![]() ,
,
![]() ≈2.08441,2n≥4.16882
≈2.08441,2n≥4.16882
由于2n为偶数,因此取6,即应有7个结点。也可以用以下公式来做。
∣R(Sn)∣=![]() ∣
∣![]() ∣≤
∣≤![]() ≤
≤![]() ,
,
h≤0.1×![]() ≈0.23876,n=2k=1/h≈4.1883, (h=(b-a)/n)
≈0.23876,n=2k=1/h≈4.1883, (h=(b-a)/n)
区间数k=3,结点数为2k+1,即应取7个结点。在实际应用中,一般取区间数k=4,则应该有9个结点。
(a=x0<x1<x2,x2<x3<x4,x4<x5<x6,x6<x7<x8=b)
注: ![]() =
=![]() ,h=
,h=![]()