6 常微分方程的数值解法

§6.1　引 言

在许多自然科学与工程技术领域中，所建立的数学模型大多是常微分方程或常微分方程组，有些问题往往很复杂，除了少数特殊类型的方程能用解析方法求得其精确解外，多数情况要找出解的解析表达式是极其困难的，甚至是不可能的。因此，只能用近似方法求得其解。近似的求解方法有两类，一类称为近似解析方法，如级数解法，逐次逼近法等；另一类称为数值解法，它可以给出解在一些离散点上的近似值。利用计算机解常微分方程主要使用数值方法。

首先考虑一阶常微分方程初值问题， 　 　　　 (6.1)

在区间［a，b］上的解。

在使用数值解法之前，首先需要考虑解的存在性。因为如果问题(6.1)没有解，即使利用数值方法可以求得一些数据也是毫无意义的。在解存在的情况下，还必须保证初值问题具有惟一的解。由常微分方程理论中，关于解的存在惟一性有如下定理。

定理 设在区域D＝上有定义且连续，并且关于y满足如下的李普希茨(Lipschitz)条件：

　 (6.2)

则对，初值问题在区间［a，b］上存在惟一的连续可微解y(x)。式(6.2)中的L称为李普希茨常数。

在对y可微的情况下，若偏导数有界，则可取：

这时李普希茨条件显然成立：

这里介于y和y*之间。这是验证公式(6.2)是否满足的最简便的方法。

除了保证初值问题有解外，还必须保证微分方程本身是稳定的。所谓稳定是指在初值问题(6.1)中，初始值y₀及微分方程的右端函数有微小的变化时，只能引起解的微小变化。这种性质对于数值求解过程来说是十分必要的，这是由于在许多实际问题中，初始值及右端函数通常是经过测量得到的，难免产生误差。在稳定的情况下，上述误差对解的影响是有限的。这对数值解法来说，显然是一个有利的条件，因为解的数值近似，完全可能引入上述种类的误差。在稳定的情况下，只要把这些误差控制得很小，就能使解达到所需要的精确度是可以期望的。

若y(x)是初值问题(6.1)的解，对方程两边积分，利用初始条件可得：

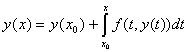　　 (6.3)

容易验证，式(6.3)是与式(6.1)等价的积分方程，我们可从式(6.3)出发构造式(6.1)数值解法的求解公式。

所谓初值问题(6.1)的数值解法，就是能算出精确解y(x)在自变量x的一系列离散结点：a≤x₀＜x_l＜…＜x_n≤b，上的近似解的数值y₀，y₁，…，y_n，这里把y_k(k＝1，2，…n)叫做初值问题在点列x_k上的数值解，其精确值为：y(x_k)(k＝1，2，…n)。数值解法的基本思想是通过某种离散化方法，将微分方程转化为差分方程(代数方程)来求解。我们用⊿x_k＝x_k－x_k－1表示求解时的步长，一般取等步长，用字母h表示。本章中在x_n处，初值问题的理论解（精确解）用y(x_n)表示，数值解法的近似解用y_n表示，并记f_n＝f(x_n，y_n)，它和f(x_n，y(x_n))是不同的，后者表示(x_n)（精确解）。

求初值问题的数值解一般是逐步进行的，即计算出y_n之后再计算y_n＋1。这些数值方法有单步法与多步法之分。单步法是在计算y_n＋1时，只利用y_n，而多步法在计算y_n＋1时，不仅要用到y_n，还要用到y_n－1，y_n－2，…等等。一般k步方法要用到y_n，y_n－1，…，y_n—k＋l。

单步法和多步法还有显式方法和隐式方法之分。显式单步方法可以写成：

y_n＋l＝y_n＋h(x_n，y_n，h) 　(6.4)

隐式的单步方法可以写成：y_n＋l＝y_n＋h(x_n，y_n，y_n＋1，h) 　　　(6.5)

每步都要解一个关于y_n＋l的方程。

对于多步法来说，显式和隐式方法的意义与单步法类似。