6．2 Euler的方法
Euler方法是常微分方程初值问题数值方法中最简单的方法。Euler方法精度低，较少有直接使用。但我们通过Euler方法介绍离散化途径、数值解法中的基本概念、术语和加速方法等。
2.1 显式Euler方法
设节点为
。初值问题（1.1）、（1.2）的显式Euler方法为
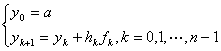（2.1）其中
。
显式Euler方法可以用多种途径导出。
导出方法1：Taylor展开法。
将
在
点进行Taylor展开,得
（2.2）忽略
这一阶项,分别用
近似
，和
，得
。结合初值条件
即得（2.1）。
导出方法 2：向前差分近似微分法。
用向前差分
近似微分
，得
（2.3）
将近似号改作等号，用
近似，，并结合初值条件即得（2.1）。
方法3：左矩数值积分法。
将（1.1）两边从
到
积分得
（2.4）
用
，
近似、，数值积分采用左矩公式得
，从而亦得（2.1）
Euler方法有几何意义，如图8-1，式（1.1）,(1.2)的解曲线
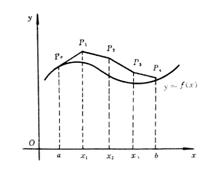
过点
，且具斜率
。从
出发以为斜率作直线
段，交
于
，显然
。式（1.1）过的解曲线具有斜率
从
出发以为斜率作直线要交
于
，余类推。这样我们得到了一条折线
，它在点
的右侧具有斜率
，与（1.1）过的解曲线相切。我们取折线，作为（1.1）、（1.2）解曲线
的近似曲线，所以Euler方法又称折线法。
2.2
隐式
Euler方法和梯形方法
若将在
展开
、
忽略
项，用
和
分别近似，及
，可以得另一计算公式
（2.5）
（2．5）式称为隐式Enler方法。隐式Euler方法也可以利用向后差分近似微分或用右矩数值求积公式来建立。读者可自行推导。
隐式 Euler方法(2.5)给出了要满足的方程，要通过解方程才能得到。
在显式和稳式Euler方法中，忽略的项都是项，为了得到更高精确度的方法，我们可将
取平均得
当三次连续可微时,
。忽略
项，用分别近似
，得：
（2.6）
（2.6）称为梯形方法。取这个名称的原因是利用梯形求积公式
其中
表示关于
的全微分，忽略数值求积余项也可建立（2.6）。
梯形方法也是隐式方法，要通过解（2.6）来得到。
与（1.10）式中单步法公式相对应，显式Euler方法取：
隐式Euler方法取
梯形方法取：
当
在
上满足基本条件，关于
的Lipschitz常数为
时，只要
确定了唯一的
；同样，只要
（2.6）确定了唯一的。以（2.6）为例，当以为变量的函数
在
上关于满足Lipschitz条件，且Lipschitz常数为
从而由第七章压缩不动点定理得方程
有唯一点不动
而且从任意
出发，迭代
（2.7）
都收敛到
在实际计算中总希望有较好的
，用较少的迭代步，取得有足够精度的。
2．3 预估 – 校正Euler方法
在实际计算中，
的计算量比较大，往往取
作为来用。我们称
为
的
次迭代改进。最常用的方法之一是先用显式Euler方法所得的
为，再用梯形方法改进一次
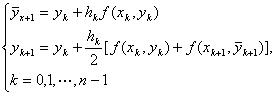（2.8）
方法（2.8）称为预估-校正Euler方法，或改进Euler方法。预估-校正Euler方法还可写成
（2.9）
或
（2.10）
例1 用显式Euler方法，梯形方法和预估-校正Euler方法解初值问题
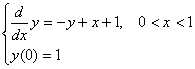
解 取
，Euler方法为
梯形方法为 
预估-校正Euler方法为
计算结果与准确解
比较表明，梯形方法和预估-校正Euler方法比显式Euler方法有更好的精度。
2．4 单步法的局部截断误差、整体截断误差
设所用单步法为
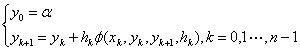(2.11)
定义2 设是(1.1)、(1.2)的准确解,称
(2.12)
为单步法(2.11)在的局部截断误差.
定义3 设是(1.1)、(1.2)的解,
是单步法(2.11)的数值解,称
为单步法(2.11)在点的整体截断误差;如果对充分小的
成立
(2.13)
常数
独立于
,就称方法(2.11)是
阶方法.
定理4 若单步法(2.11)的局部截断误差是
阶的,即
独立于，而且函数
在区域
上关于
满足条件：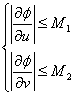
（2.14）
则单步法（2.11）是阶方法。
证明 由（2.12）和(2.11)得
即
在上式中，我们假设
（对显式方法来说
任意）。令
，简单推导可得
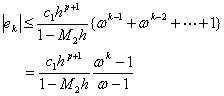
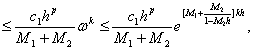
因此我们有
当
时，
，其中
当在上满足基本条件时，单步法的收敛阶总是由局部截断误差的阶来确定的。
对显式Euler方法来说，当解二阶连续可导时，其局部截断误差为
若关于满足Lipschitz连续条件，Lipschitz常数为，则
从而显Euler方法是一阶方法。
对隐式Euler方法来说，可得
对梯形方法，具局部截断误差为
因此其整体误差满足
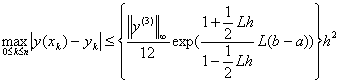
梯形方法是二阶方法。
分析局部截断误差的一种方法是利用Taylor级数展开法。若有
（2.15）
则称
为局部截断误差的主项。若局部截断误差的主项是的次幂项，则单步法是阶方法。
分析预估-校正Euler方法的局部截断误差可以知道该方法是二阶方法。