6.3. Runge-Kutta法
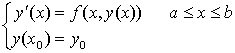
构造微分方程的数值解法的一个准则是误差要小。从误差分析的过程中,可能得到更好的方法。
一、Taylor级数法
![]()
将上式中![]() 的各阶导数用
的各阶导数用![]() 来表出,可以得到计算
来表出,可以得到计算![]() 的各阶方法。
的各阶方法。
例:Euler方法![]() 的误差分析。
的误差分析。
例:改进的Euler方法
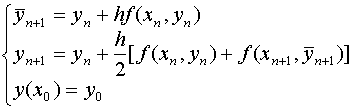
的误差分析。
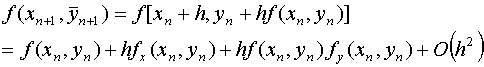
二、Runge-Kutta法
分析Euler方法及其改进方法和梯形方法的几何解释,可知关键在于对平均斜率的估计。
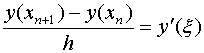 ,所以
,所以![]()
Euler方法简单地取点![]() 的斜率值
的斜率值![]() 作为平均斜率。
作为平均斜率。
改进的Euler方法可写成
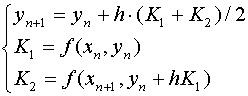
可见改进的Euler公式可以这样理解,它用![]() 与
与![]() 两个点的斜率值
两个点的斜率值![]() 与
与![]() 取算术平均作为平均斜率,而
取算术平均作为平均斜率,而![]() 处的斜率值
处的斜率值![]() 则通过已知
则通过已知![]() 信息来预测。
信息来预测。
这个处理过程启示我们,如果设法在![]() 内多预测几个点的斜率值,然后将它们加权平均作为平均斜率,则有可能构造出具有更高精度的计算公式。这就是Runge-Kutta方法的基本思想。
内多预测几个点的斜率值,然后将它们加权平均作为平均斜率,则有可能构造出具有更高精度的计算公式。这就是Runge-Kutta方法的基本思想。
1. 二阶Runge-Kutta方法(用两个点的斜率平均作为平均斜率)
取![]()
![]() ,
,
![]() ,
,
![]() ,
,
当然![]() 的值需要预测
的值需要预测![]() (相当于Euler公式)得格式
(相当于Euler公式)得格式
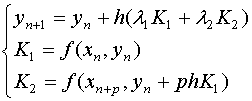
将![]() 及
及![]() 展开之后,比较
展开之后,比较![]() 与
与![]() ,可知欲使上式有二阶精度,只要成立
,可知欲使上式有二阶精度,只要成立
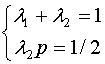
解得![]() 之后,得二阶Runge-kutta公式,有无数个,包括改进的Euler方法(p=1),另外常见的还有(p=1/2)
之后,得二阶Runge-kutta公式,有无数个,包括改进的Euler方法(p=1),另外常见的还有(p=1/2)
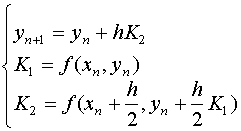
不可能达到三阶
2. 三阶Runge-Kutta方法(用三个点的斜率平均作为平均斜率)
取![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 的值用
的值用![]() 来预测(相当于Euler公式)
来预测(相当于Euler公式)
![]() 的值用
的值用![]() 来预测,得格式
来预测,得格式

将![]() ,
,![]() ,
,![]() 展开,比较
展开,比较![]() 与
与![]() ,可得上式中各待定系数所满足的关系,
,可得上式中各待定系数所满足的关系,
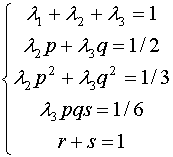
从而可得到三阶精度的Runge-Kutta公式。其中较常见的有(p=1/2,q=1)
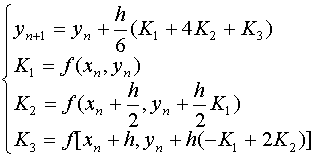
(p=1/2,q=3/4)
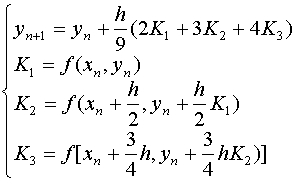
不可能达到四阶
3. 四阶Runge-Kutta公式(用四个点的斜率平均作为平均斜率)
最常见的(经典)Runge-Kutta公式
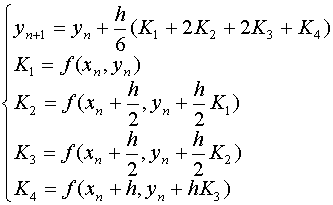
取5,6,7个点时,最高只能达到4,5,6阶,取8,9个点时,只能达到6,7阶,取10个以上点时,只能达到8阶。故四阶方法是最常用的。
例:使用三阶、四阶R-K法解下列初值问题,取h=0.1, 求![]()
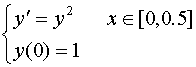
function y=rk4(myfun,x0,y0,h,x)
%x-x0 should be n times
of h
n=round((x-x0)/h);
xi=x0;y(1)=y0;
for i=1:n
k1=feval(myfun,xi,yi);
k2=feval(myfun,xi+h/2,yi+h*k1/2);
k3=feval(myfun,xi+h/2,yi+h*k2/2);
k4=feval(myfun,xi+h,yi+h*k3);
y(i+1)=y(i)+h*(k1+2*k2+2*k3+k4)/6;
xi=xi+h;
end