6．4 线性多步方法

在前面所讨论的方法中，在计算时只用到的信息(单步法)，为提高截断误差的阶，第个时间步必须增加计算右端函数的次数。当的结构比较复杂时，计算量较大。现在指出另一个提高截断误差阶的办法，即构造这样的方法，在计算公式中，充分利用前几步得到的信息及…，但每进一步，只计算一次的值。这样的方法称为多步方法，若函数值以线性组合的形式出现于公式中，则称方法为线性多步方法。

一、线性多步方法的构造

构造多步法有多种途径，常用的有基于数值积分的构造方法和基于Taylor展开的构造方法(待定系数法)，以下主要介绍待定系数法。

1. 数值积分法的主要思想

为要通过这个积分关系式得到的近似值，只要近似地算出其中的积分项，而选用不同的数值方法计算这个积分项，就会导出不同的计算公式。我们知道，基于插值原理可以建立一系列的数值积分方法，运用这些方法可以导出求解微分方程的一系列计算公式。为要运用插值方法，关键在于选取合适的插值节点。

例如在上使用作为节点作函数的插值多项式，(以为函数值的近似)，从而得到计算公式(三步显式Adams方法)

选取作为插值节点时，将导致隐式Adams方法。

2. 待定系数法

在单步法中，计算时只用到。考虑到计算之前已得到一系列节点等上的斜率值，能否利用这些已有的信息来减少计算量呢？由，采用两点的斜率加权平均作为的近似，得

，其中

选取适当的系数使得上式具有高的精度。将，在处展开，比较，可得

时，，即具有2阶精度。此时

，二阶Adams格式。

类似地，若采用三点的斜率加权平均作为的近似，即

将在处展开，比较，当

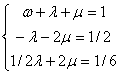
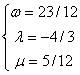
时，有三阶精度。

，三阶Adams格式。

，四阶Adams格式。

以上Adams格式都是显式的，但是用处的斜率来预报区间上的平均斜率，效果不够理想。用的斜率来得出上的平均斜率，这自然会导致隐式格式。