附录

MATLAB简介

这里介绍MATLAB一些入门知识，包括MATLAB桌面和窗口，MATLAB命令格式、数据格式、数据文件和变量管理，MATLAB的数组和矩阵运算，MATLAB的字符串、元胞和结构等数据类型，MATLAB的程序设计方法，MATLAB作图方法在线帮助的使用和程序文件和目录的管理等。

表一 MATLAB的基本命令

主题词	含义	主题词	含义
format	设置数据显示格式	feval	函数求值
who	显示变量名	input	提示输入
whos	显示变量信息	disp	输出
clear	清除内存变量	tic	启动秒表
save	保存工作变量到文件	toc	时间读数（秒）
load	从文件装载变量	help	帮助
linspace	区间等分	lookfor	查找
length	获取数组长度	type	列程序清单
size	矩阵大小	which	查找文件目录
max	最大值	double	双精度
min	最小值	str2num	字符串转化为数值
sum	求和	num2str	数值转化为字符串
find	条件检索

一、MATLAB桌面

启动MATLAB后，就进入MATLAB的桌面，图1为MATLAB6.1的默认（Default）桌面。第一行为菜单栏，第二行为工具栏，下面是三个最常用的窗口。右边最大的是命令窗口（Command Window），左上方前台为发行说明书窗口（Launch pad），后台为工作空间（Workspace），左下方为命令历史（Command History）后台为当前目录（Current Directory）。

1.窗口

（1）命令窗口

该窗口是进行MATLAB操作最主要的窗口。窗口中“>>”为命令输入提示符，其后输入运算命令，按回车键就可执行运算，并显示运算结果.。

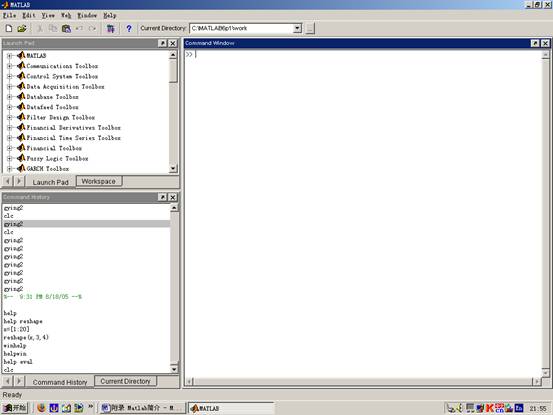
图1

（2）发行说明书窗口

发行说明书窗口是MATLAB所特有的，用来说明用户所拥有的Mathworks公司产品的工具包、演示以及帮助信息。

（3）工作空间

在默认桌面，位于左上方窗口前台，列出内存中MATLAB工作空间的所有变量的变量名、尺寸、字节数。用鼠标选中变量，击右键可以打开、保存、删除、绘图等操作。

（4）当前目录

在默认桌面，位于左下方窗口后台，用鼠标点击可以切换到前台。该窗口列出当前目录的程序文件（.m）和数据文件（.mat）等。用鼠标选中文件，击右键可以进行打开、运行、删除等操作。

（5）命令历史（Command History）

该窗口列出在命令窗口执行过的MATLAB命令行的历史记录。用鼠标选中命令行，击右键可以进行复制、执行（Evaluate Selection）、删除等操作。

除上述窗口外，MATLAB常用窗口还有编程器窗口、图形窗口等。

二、数据和变量

1.表达式

在命令窗口作一些简单的计算，就如同使用一个功能强大的计算器，使用变量无须预先定义类型。

例如，设球半径为r=2，求球的体积。

>>r=2 %表达式将2赋予变量r

r= %系统返回r的值

>>v=4/3*pi*r^3 %pi为内置常量，乘方用^表示

33.5103

几个表达式可以写在一行，用分号（；）或逗号（，）分割，用分号（；）使该表达式运算结果不显示，而逗号（，）则显示结果。也可以将一个长表达式分在几行上写，用三点（…）续行。

若需要修改已执行过的命令行，可以在命令历史中找到该命令行复制，再粘贴至命令窗口修改。也可以直接使用键盘↑↓调出已执行过的命令行修改。

2.数据显示格式

MATLAB默认的数据显示格式为短格式（short）：当结果为整数，就作为整数显示；当结果是实数，以小数点后四位的长度显示。若结果的有效数字超出一定范围，以科学计数法显示（如3.2000e-006表示）。数据显示格式可使用命令Format改变。例如：

>> format long;v %长格式，16位

v =

33.51032163829112

>> format short;v %短格式

v =

33.5103

>> format rational;v %有理格式，近似分数

v =

6501/194

3.复数

MATLAB中复数可以如同实数一样，直接输入和计算。例如：

>> a=1+2i;b=5-4*i;c=a/b

c =

-0.0732 + 0.3415i

4.预定义变量

MATLAB有一些预定义变量（表1），启动时就已赋值，可以直接使用，如前我们使用的圆周率pi和虚数单位i.

表1 常用预定义变量

变量名	说明
i或j	虚数单位
pi	圆周率3.14159…
eps	浮点数识别精度2^(-52)=
realmin	最小正实数
realmax	最大正实数
inf	无穷大
NaN	没有意义的数

预定义变量在工作空间观察不到。如果预定义变量被用户重新赋值，则原来的功能暂不能使用。当这些用户变量被清除（clear）或MATLAB重新启动后，这些功能得以恢复。

5.用户变量

MATLAB变量名总以字母开头，以字母、数字或下划线组成，区分大小写，有效字符长度为63个。如A,a,a1,a_b都是合法的，且a与A表示不同变量。在Command Window中使用的变量一旦被赋值，就会携带这个值存在于工作空间，直到被清除或被赋予新的值。

ans是系统一个特别的变量名。若一个表达式运算结果没有赋予任何变量，系统自动用ans存放答案。例如：

>> A=5+4i;b=5-4*i;B=1;A*b %没有定义A*b的输出变量

ans =

41 %ans来接受计算结果，注意这是大写A与小写b的乘积，尽管我们可以使用工作空间来查询和清除变量，但使用下列命令方式更快捷：

>> whos %查询Workspace中的变量列表

Name Size Bytes Class

A 1x1 16 double array (complex)

B 1x1 8 double array

a 1x1 16 double array (complex)

ans 1x1 8 double array

b 1x1 16 double array (complex)

c 1x1 16 double array (complex)

Grand total is 6 elements using 80 bytes

>> A %查询变量A的值

A =

5.0000 + 4.0000i

>> clear A %清除变量A

>> A %再查询A的值，已经不存在了

??? Undefined function or variable 'A'.

>> clear %清除Workspace中所有变量

>> whos %Workspace中已没有任何变量了

三、数组和矩阵运算

MATLAB基本数据单元是无需指定维数的数组。数组运算是MATLAB最鲜明的特点，一方面可以使得计算程序简明易读，另一方面可以提高计算速度。

1.数组的输入

最常用的数组是双精度数值数组（double array）。一维数组相当于向量，二维数组相当于矩阵，一维数组可以视为二维数组的特例。二维数组的第一维称为“行”，第二维称为“列”。MATLAB数组无需预先定义维数。直接输入数组的元素，用中括号（[]）表示一个数组，同行元素间用空格或逗号分隔，不同行间用分号或回车分隔，例如：

>> clear;a=[1,2,3;4,5,6;7,8,9]

a =

1 2 3

4 5 6

7 8 9

或

>> a=[1 2 3 %这种方式特别适用于大型矩阵

4 5 6

7 8 9]

a =

1 2 3

4 5 6

7 8 9

对于等差数列构造的一维数组，可用冒号运算生成，也可用函数linspace生成。

>> b=0:3:10 %初值：增量：终值

b =

0 3 6 9

>> b=0:10 %增量为1可省略

b =

0 1 2 3 4 5 6 7 8 9 10

> >b=10:-3:0 %递减

b =

10 7 4 1

>> b=linspace(0,10,4) %将区间[0，10]等分为4-1=3份

b =

0 3.3333 6.6667 10.0000

>> length(b) %查询b的长度

ans =

>> b(3) %查询b的第三个元素

ans =

6.6667

>> b([1,end]) %查询b的首和尾元素

ans =

0 10

二维数组元素双下标编址按通常方式，单下标编址按列排序。

>> size(a) %查询数组a的尺寸

ans =

3 3

>> a(3,2),a(6)

ans =

>> c=a([1 3],[2 3]) %提取a的第一、第三行和第二、第三列（分块矩阵）

c =

2 3

8 9

>> d=a(2,:) %提取a的第二行

d =

4 5 6

>> a(:) %将a所有元素按单下标顺序排为列向量

ans =

一些特殊的二维数组可以用函数产生，例如：

>> a=zeros(2,4) %生成2行4列零矩阵

a =

0 0 0 0

>> b=ones(1,4) %生成1行4列1矩阵

b =

1 1 1 1

>> c=[a;b] %拼接

c =

0 0 0 0

1 1 1 1

>> c(2,1)=100 %修改部分元素

c =

0 0 0 0

100 0 0 0

1 1 1 1

>> reshape(c,2,6) %按2行6列重排矩阵元素

ans =

0 1 0 0 1 0

100 0 1 0 0 1

注意：数组下标对应矩阵的行和列，编址一律从1开始，不能用0.

矩阵输入也可用“load”命令从外部数据文件导入

2.数组运算

数组运算是指数组对应元素之间的运算，也称点运算。矩阵的乘法、乘方和除法有特殊的数学含义，并不是数组对应元素的运算，所数组乘法、乘方和除法的运算符前特别加了一个点。特别要区分数组运算在乘法、乘方和除法上的意义和表示上与矩阵运算的不同。

表2 数组运算符

运算	符号	说明
数组加与减	A+B与A-B	对应元素之间加减
数乘数组	kA或Ak	k乘A的每个元素
数与数组加减	k+A或k-A	k加（减）A的每个元素
数组乘数组	A.*B	点运算只有点乘、点乘方、点除三个，表示对应元素之间的运算；（.）是一个整体，点(.)不能漏掉，（.）和（）之间也不能有空格
数组乘方	A.^k,k.^A
数除以数组	k./A
数组除法	左除A.\B,右除B./A

>> clear;A=[1 -1;0 2];B=[0 1;1 -1];

>> A.*B %注意不是A*B

ans =

0 -1

0 -2

>> A.\B,A./B

Warning: Divide by zero.

ans =

0 -1.0000

Inf -0.5000

Warning: Divide by zero.

ans =

Inf -1

0 -2

>> A.^2

ans =

1 1

0 4

>> 1./A

Warning: Divide by zero.

ans =

1.0000 -1.0000

Inf 0.5000

3.矩阵运算

矩阵是一个二维数组，所以矩阵的加、减、数乘等运算与数组运算是一致的。但是有两点需要注意：

（1）对于乘法、乘方和除法等三种运算，矩阵运算与数组运算的运算符及含义不同：矩阵运算按线性变换定义，使用通常符号；数组运算按对应元素运算定义，使用点运算符；

（2）数与矩阵加减、矩阵除法在数学上是没有意义的，在MATLAB中为简便起见，定义了这两类运算，其含义见表3.

表3 矩阵运算符

运算	符号	说明
转置	A'
加与减	A+B与A-B	同数组运算
数乘矩阵	kA或Ak	同数组运算
矩阵乘法	A*B
矩阵乘方	A^k
数与矩阵加减	k+A与k-A	k+A等价于k*ones(size(A))+A
矩阵除法	左除A\B，右除B/A	它们分别为矩阵方程AX=B和XA=B的解

>> A=[1 2;3 4];B=[4 3;2 1];

>> 100+A

ans =

101 102

103 104

>> A*B,A.*B %注意矩阵运算和数组运算的区别

ans =

8 5

20 13

ans =

4 6

6 4

>> A\B,B/A,A.\B,B./A %注意矩阵运算和数组运算的区别

ans =

-6.0000 -5.0000

5.0000 4.0000

ans =

-3.5000 2.5000

-2.5000 1.5000

ans =

4.0000 1.5000

0.6667 0.2500

ans =

4.0000 1.5000

0.6667 0.2500

4.数学函数

数组的数学函数也是按每个元素的运算，使用通常的函数符号，常用数学函数见表4

表4 数学函数

函数	意义	函数	意义
sin	正弦	fix	向0取整
cos	余弦	mod	模余
tan	正切	rem	除法余数
cot	余切	abs	绝对值（模）
asin	反正弦	exp	指数函数
acos	反余弦	log	自然对数
sqrt	开方	log10	以10为底的对数

>> A=[4 -1;3 2];

>> B=exp(A)

B =

54.5982 0.3679

20.0855 7.3891

>> C=fix(B)

C =

54 0

20 7

>> D=sin(C)

D =

-0.5588 0

0.9129 0.6570

>> E=log(D)

Warning: Log of zero.

E =

-0.5820 + 3.1416i -Inf

-0.0911 -0.4201

5.关系与逻辑运算

MATLAB的关系运算和逻辑运算符都是对于元素的操作，其结果是特殊的逻辑数组（logical array）表5，“真”用1表示，“假”用0表示，而逻辑运算中，所有非零元素作为1（真）处理。

表5 关系运算和逻辑运算

运算符	含义	运算符	含义
<	小于	&	与
<=	小于等于	\|	或
>	大于	~	非
>=	大于等于	all
= =	等于	any
~=	不等于

>> A=-2:4,B=4:-1:-2

A =

-2 -1 0 1 2 3 4

B =

4 3 2 1 0 -1 -2

>> A>B

ans =

0 0 0 0 1 1 1

>> A==B

ans =

0 0 0 1 0 0 0

>> A&B %逻辑运算中，所有非零元素作为1（真）处理

ans =

1 1 0 1 0 1 1

>> A|B

ans =

1 1 1 1 1 1 1

>> find(abs(A)>=2) %返回绝对值大于或等于2的元素的下标

ans =

1 5 6 7

>> any(abs(A)>5) %若存在绝对值大于5的元素，返回1

ans =

>> all(abs(A)>5) %若所有元素绝对值大于5，返回1

ans =

四、字符串、元胞和结构

除数值（double）以外，常用的数据类型还有字符(char)、元胞(cell)和结构(structure)，由此进一步组成字符数组(char array)、元胞数组（cell array）和结构数组（structure array）.

1.字符串

MATLAB字符串用单引号对来标识，其数据类型为字符数组。

>> a1='Hello everyone'

a1 =

Hello everyone

>> a2='各位好' %注意单引号，不是双引号

a2 =

各位好

>> a=[a1,'.',a2,'.'] %字符串拼接

a =

Hello everyone.各位好.

>> size(a)

ans =

1 19 %共19个字符

>> double(a)

ans =

Columns 1 through 8

72 101 108 108 111 32 101 118

Columns 9 through 16

101 114 121 111 110 101 46 47351

Columns 17 through 19

52923 47811 46 %中文ASCII码很大

>> a=char(ans)

a =

Hello everyone.各位好.

数字字符串与数值之间也可以用num2str和str2num转换。一个数组的元素要么都是数值，要么都是字符串，数值转换后可以与字符串出现在同一数组中。

>> a=12;b=sqrt(a);

>> ['a=',num2str(a),',a的开方=',num2str(b)]

ans =

a=12,a的开方=3.4641

MATLAB命令可以定义成一个字符串，使用eval可以使该字符串所表达的MATLAB命令得到执行。

>> fun='x.^2.*sin(x)';

>> x=1;eval(fun)

ans =

0.8415

>> x=1:3;eval(fun)

ans =

0.8415 3.6372 1.2701

2.元胞和结构

不管是数值数组还是字符数组，其数据结构必须是整齐的。首先数值和字符不能混合，其次小数组拼接成大数组时，其尺寸(size)必须相符(agree)。例如：

>> A=['first';'second'] %错误

??? Error using ==> vertcat

All rows in the bracketed expression must have the same

number of columns.

将不同类型、不同尺寸的数组，加大括号（{}），可构成一个元胞。几个元胞可以构成元胞数组。

>> Ac1={'first';1:3};Ac2={'second';[1 2;3 4]};

>> Ac=[Ac1,Ac2]

Ac =

'first' 'second'

[1x3 double] [2x2 double]

>> size(Ac)

ans =

2 2

>> Ac(2,1) %小括号，查询Ac的第二行第一列元素

ans =

[1x3 double]

>> Ac{2,1} %大括号，查询Ac的第二行第一列元素的具体内容

ans =

1 2 3

一个结构通过“域”来定义，比元胞更丰富、更灵活。几个结构可以合成一个结构数组，但这些结构的域名必须一致。

>> As1.f1='first';As1.f2='second';As2.f1=1:3;As2.f2=[1 2;3 4];

>> As=[As1;As2]

As =

2x1 struct array with fields:

>> size(As) %注意其size结果与元胞数组不同

ans =

2 1

>> As(2,1).f1

ans =

1 2 3

>> As.f1

ans =

first

ans =

1 2 3

元胞数组与结构数组可以用struct2cell和cell2struct函数进行适当的转换。

>> Bc=struct2cell(As) %注意结果与Ac的不同

Bc =

'first' [1x3 double]

'second' [2x2 double]

>> Bs=cell2struct(Ac,{'one','two'},1) %定义域名，并指定取域名的维

Bs =

2x1 struct array with fields:

one

two

看一看Workspace有哪些类型，并观察其字节数。

五、程序设计

1.控制流

前面我们用的命令都是顺序结构的，对于复杂的计算，需要循环和分支等复杂的程序结构。MATLAB控制流语法都以end结尾。常用控制流见表6.

表6 MATLAB常用控制流

类型	语法	解释
循环语句	for 循环变量=数组，命令组 end	对于循环变量依次取数组中的值，循环执行命令组直到循环变量遍历数组。数组最常用的形式是初值：增量：终值
循环语句	while 条件式，命令组 end	当条件式满足，循环执行命令组直到条件不满足。使用While语句要注意避免出现死循环
分支语句	if 条件1，命令组1； elesif 条件2，命令组2； ……； else, 命令组k； end	如果条件式1满足，则执行命令组1，且结束该语句；否则检查条件式2，若满足则执行命令组2，且结束该语句；……；若所有条件式都不满足，则执行命令组k，并结束该语句。最常用的格式是 if 条件式命令组 end
分支语句	switch 分支变量 case 值1，命令组1； case 值2，命令组2； ……； otherwise 命令组k； end	若分支变量的取值1，则执行命令组1，且结束该语句；若分支变量的取值2，则执行命令组2，且结束该语句；……若分支变量不取所列出的值，则执行命令组k
中断语句	pause	暂停执行，直到击键盘，pause(n)为暂停n秒后再继续
中断语句	break	中断执行，用在循环语句内表示跳出循环
中断语句	return	中断执行该程序，回到主调函数或命令窗口
中断语句	error(字符串)	提示错误并显示字符说明

例1 计算

>> clear;s=0;

>> for n=1:100

s=s+1/n/n;

end

>> s

s =

1.6350

2.M脚本文件

复杂程序结构在命令窗口调试保存都不方便，所以进行复杂的运算大都使用程序文件。从命令窗口用命令“edit”就进入MATLAB的程序编辑器窗口，用以编写用户的M文件。M文件可分为两类：M脚本文件和M函数文件。

将多条MATLAB语句写在编辑器中，并以.m文件保存在适当的目录中（这个目录须为MATLAB的搜索目录），就得到一个M脚本。如我们将例1中的几条语句写在编辑器中，

保存为naega_1，然后在命令窗口执行：

>>naega_1

1.6350

执行M脚本文件也可以在程序编辑器的Debug菜单选Run。使用编辑器也可打开和修改M文件、观察变量值、调试程序等。

注意：M文件名一律以字母开头，以字母、数字或下划线组成，不要含有空格、减号等，并要防止它与系统的变量名、系统内部的M函数名冲突。例如1.m,ega-1.m,ega.1.m都是不合法的。另外，别忘了每次修改程序后都要存盘。

3.M函数文件

M脚本文件没有参数传递功能，当我们需要修改程序中的某些变量值，必须修改M文件。而M函数文件使得我们可以进行参数传递。

M函数文件以function开头，格式如下：

function 输出变量=函数名（输入变量）

语句

例如，写函数文件：

% M函数naega_1f.m

function s=f(m)

s=0;

for n=1:m

s=s+1/n/n;

end

保存为naega_1f.m，在命令窗口执行：

>>clear;naega_1f(100),naega_1f(1000)

ans=

1.6350

ans=

1.6439

注意：在MATLAB中，使用M函数是以该函数的磁盘文件主名调用，而不是文件中的函数名，但为了增强程序可读性，最好两者同名。

M函数不能像M脚本那样在编辑器窗口用Debug\run执行，因为M函数必须给予输入参数值。M函数常常被M脚本或其他M函数调用。

4.函数句柄和内嵌函数

M函数除了直接用其函数名调用之外，也可以作为一个参数调用。调用时使用所谓函数句柄(handle)方式。MATLAB命令feval用于执行函数的参数方式。例如：

>>fname=@naega_1f;feval(fname,1000)

ans=

1.6439

比较简单的函数表达式可以不用写成外部M函数，而是用更简捷的内嵌（inline）函数方式。inline的使用格式如下：

fun=inline(expr,arg1,agr2,…) expr为函数表达式字符串，arg1,arg2,….为自变量名字符串

例如：

>> fname=inline('sum(1./(1:n).^2)','n')

fname =

Inline function:

fname(n) = sum(1./(1:n).^2)

>> feval(fname,1000)

ans =

1.6439

5.其他

（1）注释

为了增强程序的可读性，程序中常常需要注释语句。M文件开头一般应有一段注释。注释用%开头，顶格书写，对本行后面字符起作用，说明文件的功能和使用方法。注释语句不参与运算，只起说明作用。使用Help可看到。注释符（%）也常用于程序调试。

（2）对话

Input在交互式执行程序中用于提示键盘输入，Disp用于屏幕显示。

例2 编写一个脚本文件，使对键盘提示输入的向量求得元素总和。

% M文件naega_2.m

%用途：本程序提示输入一个向量，并求得元素总和

%用法：输入向量用中括号，元素之间用逗号

clear A;

A=input('Enter a vector:');

d=sum(A);

disp(['The sum is',num2str(d)]);

然后在命令窗口执行：

>>naega_2

Enter a vector:[1 2 3 4]

The sum is 10

>>help naega_2

用途：本程序提示输入一个向量，并求得元素总和

用法：输入向量用中括号，元素之间用逗号

(4)子函数

M函数中允许使用子函数。M函数中第一个function为主函数，其他function为子函数。子函数只能被同一文件的主函数和其他子函数调用，不能被外部函数调用。

（5）全程变量与局部变量

M函数中所有变量为局部变量，而脚本文件中所有变量同命令窗口的命令一样都是全程变量。M函数变量值传递主要通过其输入输出变量，但也可以用global定义全程变量。它的意义与普通全程变量稍有区别，只对有定义的文件起作用。

（6）nargin与nargout

在M函数内，nargin表示该函数的输入变量个数，nargout表示该函数的输出变量个数。

（7）提高速度

MATLAB软件主要缺点是执行循环语句时速度慢。好的M程序文件应尽量使用数组运算和内部函数，少用循环语句，以提高运算速度。尽管MATLAB数组无须定义尺寸，但经常改变数组尺寸会影响速度，采取一些预分配方法可提高运算速度。另外，减少运行过程中不必要的结果显示也可提高速度。

（8）强行中断

使用快捷键Ctrl+C可以强行中断程序运行。

例3 编写一个M函数，对于任意输入的向量x，可以计算下列分段函数值构成的向量：

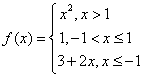
%M函数naega_3a.m

function y=naega_3a(x)

n=length(x);

for i=1:n

if x(i)>1

y(i)=x(i)^2;

elseif x(i)>-1

y(i)=1;

else

y(i)=3+2*x(i);

end

%M函数naega_3b.m

function y=naega_3b(x)

y=zeros(size(x));

k1=find(x>1);y(k1)=x(k1).^2;

k2=find(x>-1&x<=1);y(k2)=1;

k3=find(x<=-1);y(k3)=3+2*x(k3);

程序naega_3a.m是按通常思路所编程序，可读性好，但速度慢。程序naeag_3b.m是根据MATLAB数组运算设计的程序，程序简短且速度快，数组维数越高，效率改进越显著。下列程序中tic表示计时开始，toc为读数。

>>clear;tic;x=-2:0.0005:2;y=naega_3a(x);toc %时间因电脑不同而有区别

elapsed_time =

1.0400

>> clear;tic;x=-2:0.0005:2;y=naega_3b(x);toc

elapsed_time =

0.4400

六、作图

表7 常用作图命令和函数

主题词	含义	主题词	含义
plot	基本二维图形	clabel	等高线高度标志
fplot	一元函数图像	grid	格栅
ezplot	画二维曲线的符号命令	hold	图形保持
plot3	空间曲线	axis	定制坐标轴
meshgrid	网格数据生成	view	改变视点
mesh	网面图	subplot	子图
surf	曲面图	figure	新图形窗口
contour	等高线图	clf	清除图形
contour3	三维等高线图	close	关闭图形窗口
title	标题	ylabel	y轴说明
xlabel	x轴说明	zlabel	z轴说明

1.曲线图

plot(x,y) 作出以数据(x(i),y(i))为节点的折线图，其中x,y为同长度的向量

fplot('fun',[a,b]) 作出函数fun在区间[a,b]上的函数图，fun可以是M函数主名，也可是字符串

ezplot(fun,lims) 绘制字符串fun（可是显函数、隐函数或参数方程）指定的函数

plot3(x,y,z) 空间曲线图，其中x,y,z为同长度向量

>> plot([1 4 2 5],[1 3 -1 2])

依次将（1，1），（4，3），（2，-1），（5，2）连接起来得一条折线（图2）

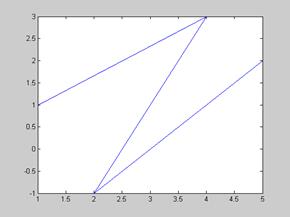
图2

图形显示在图形窗口。在图形窗口可以使用File菜单保存(Save)为M文件，导出(Export)为图形文件。也可利用图形窗口Edit菜单Copy figure作为图片复制到剪贴板，从而进一步粘贴到Word或其他应用程序中。

图形的线型、标记、颜色均可根据要求设定。常用的见表8

表8 图形元素设定

颜色		线型		标记
b	蓝（默认）	-	实线（默认）		无标记（默认）
g	绿	：	虚线	.	点
r	红	-.	点划线	o	圈
m	洋红	--	划线	x	叉
y	青			+	十字
k	黑			*	星

例4 两个一元函数和在区间-1<x<2的复合图。

% M文件naega_4.m

fplot('x^3-x-1',[-1,2]);

hold on; %在作下一幅图时保留已有图像

x=-1:0.2:2;

y=abs(x).^2.*sin(5*x); %注意数组运算

plot(x,y,':ro');

hold off; %释放hold on

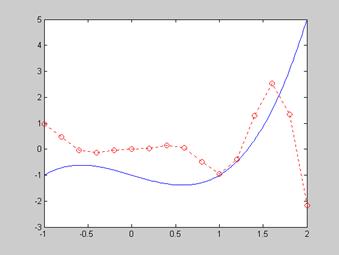
2.曲面图

[x,y]=meshgrid(xa,ya) 当xa,ya分别为m维和n维行向量，得到x和y均为n行m列矩阵。meshgrid常用于生成X-Y平面上的网格数据

mesh(x,y,z) 绘制网面图，是最基本的曲面图形命令，其中x,y,z是同阶矩阵，表示曲面三维数据

surf(x,y,z) 绘制曲面图，与mesh用法类似

contour(x,y,z) 绘制等高线图，与mesh用法类似

contour3(x,y,z) 绘制三维等高线图，与mesh用法类似

例如：

>> xa=6:8;ya=1:4; %生成x,y各自的节点

>> [x,y]=meshgrid(xa,ya); %生成X-Y面上网格

>> z=x.^2+y.^2; %计算X-Y面上各网格点的z轴高度

>> mesh(x,y,z)

>> [x,y,z]

ans =

6 7 8 1 1 1 37 50 65

6 7 8 2 2 2 40 53 68

6 7 8 3 3 3 45 58 73

6 7 8 4 4 4 52 65 80

这3组数据构成空间网面的12格点坐标

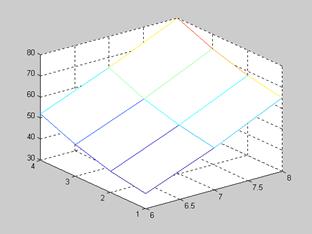
例5 二元函数图

%M文件 naega_5.m

clear;close; % close关闭当前图形窗口

xa=-2:0.2:2;ya=xa;

[x,y]=meshgrid(xa,ya);

z=x.*exp(-x.^2-y.^2);

mesh(x,y,z);pause %网格图，pause暂停直到按任意键

surf(x,y,z);pause %网面图

contour(x,y,z);pause %等高线图

contour(x,y,z,[0.1 0.1]); %z=0.1的一条等高线

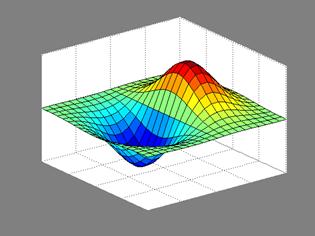
3.图形说明和定制

title('字符串') 图形标题说明

xlabel,ylabel,zlabel 用法类似于title，分别说明坐标轴x,y,z

grid on/off 显示/不显示格栅

box on/off 使用/不使用坐标框

hold on/off 保留/释放现有图形

axis off/on 不显示/显示坐标轴

axis([a,b,c,d]) 定制二维坐标轴范围 a<x<b,c<y<d

axis([a,b,c,d,e,f]) 定制三维坐标轴范围 a<x<b,c<y<d,e<z<f

figure 开一个新图形窗口

close 关闭现有图形窗口

subplot(m,n,k) 将图形窗口分为m*n个子图，并指向第k幅图

legend(str1,str2,……) 图例，字符串str1,str2,……依次为各图形对象说明

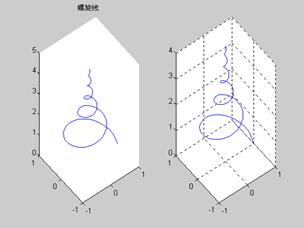
例6 由参变量函数表示的空间曲线

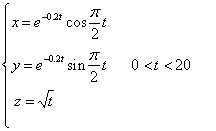
%M文件naega_6.m

clear;close;

t=0:0.1:20;r=exp(-0.2*t);th=0.5*pi*t;

x=r.*cos(th);y=r.*sin(th);z=sqrt(t);

subplot(1,2,1)

plot3(x,y,z);

title('螺旋线');

subplot(1,2,2)

plot3(x,y,z);

axis([-1 1 -1 1 0 4])

grid on;

七、在线帮助和文件管理

1.在线帮助

help 显示MATLAB主题目录

help 子目录名显示子目录中所有MATLAB系统命令及函数

help 命令或函数显示该命令或函数的说明部分

lookfor 关键字显示与该关键字有关的命令和函数

type M文件名显示M文件程序代码

which M文件名显示指定的MATLAB文件的路径

demo 演示MATLAB功能

MATLAB提供了两种形式的帮助系统：纯文本帮助、HTML帮助。纯文本帮助是最常用、最经济的在线帮助，不需要另外安装，是边用边学计算机软件的最有效的方法。

>>help %显示MATLAB及其工具箱的主题目录，其中有graph3d

>>help graph3d %显示3维图形主题目录内所有M命令和函数，其中有mesh

>>help mesh %显示M函数mesh的用法说明，即其M文件的注释部分

>>which mesh %显示M函数mesh所在的目录

>>type mesh %显示函数mesh的M文件程序代码

>>lookfor surface %显示MATLAB搜索路径中凡是第一行注释含surface的M命令和函数，其中有函数mesh

若我们现在要解决一个线性规划问题，但不知道怎么用MATLAB求解，可利用线性规划的关键字programming:

>>lookfor programming

可以找到有关programming的很多命令，其中有一个LINPROG是线性规划（Linear programming）.再用：

>>help linprog

可以得到使用linprog解线性规划问题用法的详细说明。进一步使用：

>>type linprog

可以看到linprog的M文件程序代码。

2.文件和目录管理

MATLAB文件有M、Mat、Mex等。其中M文件是最重要的，MATLAB绝大多数内部命令和函数是M文件，用户自编的程序一般也是M文件。MATLAB只执行当前目录(Current Directory)和搜索路径（写在文件pathdef.m）中的M文件。

初学者在M文件的保存上经常出现下列几种错误：

（1）文件修改后没有保存；

（2）文件保存的目录不在当前目录和MATLAB搜索路径中；

（3）文件名使用了常数或内存中的变量，如1.m,pi.m等；

（4）文件名用了减号、空格等非法字符，如eg2-1.m,eg2.1.m等；

（5）文件名与MATLAB内建(build-in)函数和其他内部函数冲突，如mesh.m,fitfun.m等。